ベイズ分位点回帰
bayes: qreg コマンドは、ベイズ分位点回帰に適合します。
分位回帰は、結果の条件付き分位を予測子の線形結合としてモデル化します。
従来の分位点回帰は、特定の損失関数と線形計画法に依存しています。
ベイズ分位点回帰を導入するために、Yu と Moyeed (2001) は、
尤度関数に非対称ラプラス分布を仮定する分位点回帰と同等の定式を使用しています。
ベイズ分位点回帰は、この尤度関数をモデルパラメーターの事前分布と組合せて事後モデルを形成し、
推定にマルコフ連鎖モンテカルロ (MCMC) 法を使用します。
これにより、モデルベースの「標準誤差」を含む包括的な推論のためのモデルパラメーターの完全な事後分布が提供されます。
従来の分位点回帰では、標準誤差はブートストラップまたはカーネルベースの方法を使用して計算されます。 ベイズ推定では、事後標準偏差が標準誤差の役割を果たします。 パラメトリック尤度モデルを想定すると、事後標準偏差はそのモデルに基づいて推定され、より効率的になる可能性があります。
操作例
Koenker と Bassett (1982) で説明されている Engel (1857) のデータを使用して、世帯収入と食費の関係を調べてみましょう。 分位点回帰を使用して、さまざまな分位間でこの関係を比較してみましょう。 まず、初期設定を使用して、結果変数の 50 パーセンタイルにモデルを適合させます。これは、中央値回帰と呼ばれるモデルです。 再現性のために、rseed(19) オプションを指定します。
. webuse engel1857. bayes, rseed(19): qreg foodexp income
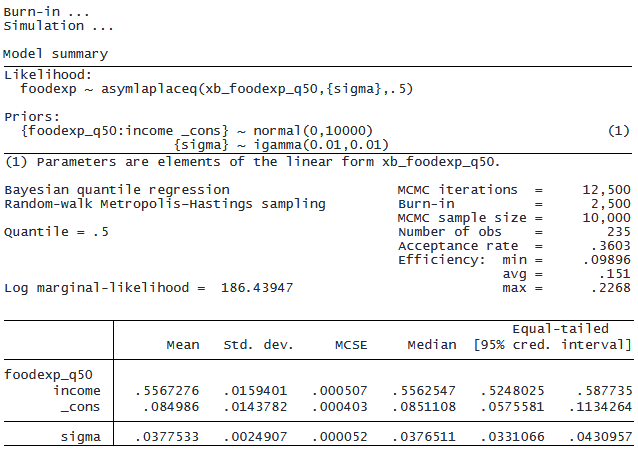
変数incomeの係数の平均事後推定値は 0.56 で、95% 信用区間 (CrI) は [0.52, 0.59] です。
次に、qreg で quantile() オプションを指定して、
結果変数の 25 パーセンタイル (または 0.25 分位) に注目します。
. bayes, rseed(19): qreg foodexp income, quantile(0.25)
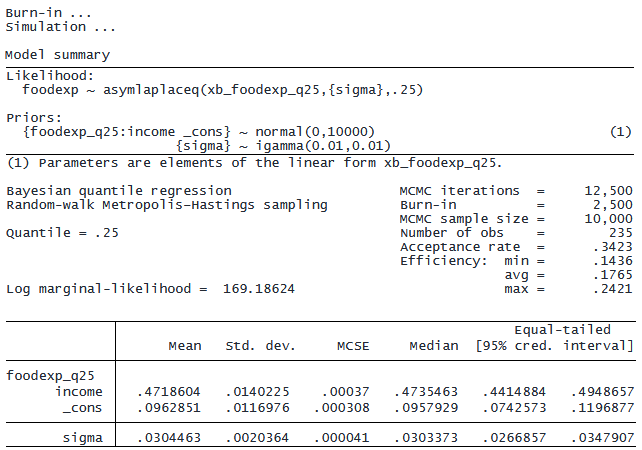
変数incomeの係数の平均事後推定値は 0.47 で、95% CrI は [0.44, 0.49] です。
2 つの分位回帰からの信用区間は重複していません。
これは、世帯収入と食費の関係が 0.25 分位と 0.50 分位で異なることを示しています。
bayes: qreg の quantile() オプションで異なる分位を指定し、
その結果を使用して以下のグラフを作成することで、この関係をさらに調べることができます。

グラフは、食費の分布 (分位) 全体にわたる世帯収入の係数の不均一性を示しています。 分位値が増加すると、係数が増加します。 (これは、世帯収入のうち食費に費やす割合が世帯収入とともに増加することを意味するものではありません。 予測を取得してエンゲル曲線を作成すると、食費の割合が世帯収入とともに減少することがわかります。)
bayes: qreg の後には、既存のすべてのベイズ事後推定コマンドを使用できます。
たとえば、foodexp の 25 パーセンタイルが区間 [0.525, 0.588] (中央値回帰モデルから得られる 95% CrI) 内となるモデル内の
世帯収入の係数の事後確率を計算できます。これを実行するには、bayestest interval コマンドを使用します。
. bayestest interval {foodexp_q25:income}, lower(.525) upper(.588)
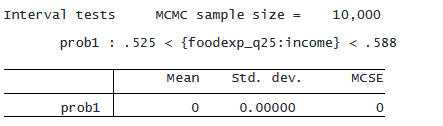
推定事後確率は 0 であり、世帯収入が食費に与える影響は 25 パーセンタイルと 50 パーセンタイルで異なることを示しています。
参考
さらに詳しい内容につきましては、下記のマニュアルをご覧ください。


