gmm
Stata の新コマンド gmm を用いることによって、非線形最小2乗法や非線形SUR回帰 (seemingly unrelated regression) と同等の簡便さで一般化モーメント法が利用できるようになりました。置換可能数式によって残差方程式を指定し、加重行列を選択すれば結果を得ることができます。
次に示すのは医者にかかった回数を示すポアソンモデルを gmm によってフィットさせた例です。説明変数としては次のものを想定しています。
- female(性別)
- income(収入)
- chronic(慢性疾患の有無)
- private(民間健康保険への加入/非加入)
なお、収入は内生変数と考えられるため、年齢 (age) と人種 (black, hispanic) を操作変数として指定しています。
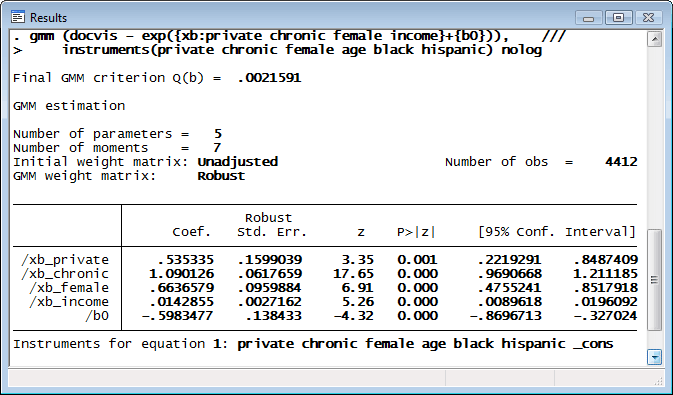
デフォルトの場合、gmm は2段階推定法、及び誤差は独立ではあるが同一分布には従わないことを仮定する加重行列を使用します。wmatrix() と vce() オプションを使用することによって、独立、同一分布に従う誤差、独立ではあるが同一分布とは言えない誤差、グループレベルのクラスタリングを呈する誤差、あるいは分散不均一で自己相関を持った誤差に対応した加重行列や分散共分散行列を要求することができます。また、標準誤差をブートストラップ法やジャックナイフ法によって算出することもできます。
GMMによってモデルのフィットを行う場合、操作変数が直交化条件、すなわち誤差と無相関であることを確認する必要があります。GMM推定においては Hansen の J 統計量が最も一般的な検定統計量です。実際、上の例では操作変数の妥当性が議論を呼びそうです。なぜなら医者にかかる回数は年齢によって影響されると考えられるからです。estat overid を用いると Hansen の J 統計量を算出することができます。

操作変数が正当なものであるとする帰無仮説のもとでは、検定統計量は χ2 分布に従います。有意な p 値から判断すると、操作変数の一部が適正ではないと言えます。
gmm の数値微分のルーチンは非常に正確であるため、多くの場合、解析的な形で導関数を指定する必要はありません。しかし性能が重要であるとか、モデルを繰返しフィットさせる計画がある場合には、解析的な導関数式は有用なものとなります。次はその一例です。
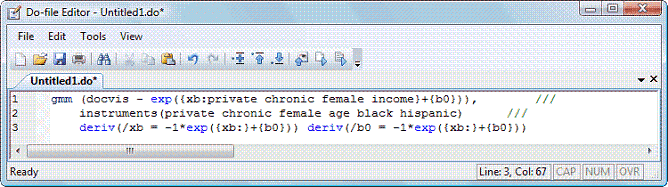
{xb:private chronic female income} という記法は変数の線形結合を作成する際の短縮形です。各項を {xb_private}*private + {xb_chronic}*chronic + {xb_female}*female + {xb_income}*income という形で明示することもできます。短縮形を使用した場合には導関数の指定も項単位ではなく、線形結合を単位に行えるようになります。線形結合が一旦宣言されると、それを単に xb: として参照することができます。
標準的な操作変数の他に、内生回帰変数を用いた動的、その他のパネルモデルで用いられるパネルスタイルの操作変数を生成させることもできます。これらのモデルにおいては通常、回帰変数のラグ値が操作変数として用いられます。利用可能なラグ値の数は時間次元の増加に伴い増大します。gmm の xtinstruments() オプションによりこれらの操作変数の生成は簡単に行えます。
より複雑な分析に対処するために、残差方程式の評価を置換可能数式ではなくプログラムで記述する機能も用意されています。その場合のプログラムの構成は ml, nl, nlsur で用いられるものと同一です。以下はモーメント評価用のプログラムを用意する形で上記ポアソンモデルのフィットを行った例です。

このプログラミングを併用した gmm は極めて柔軟性に富んでいます。指定を要する項目はモーメント方程式の数とモデル中のパラメータ数だけです。操作変数、加重行列のタイプ、標準誤差のタイプはオプションとして指定できます。


