線形回帰分析
線形回帰は、連続値のアウトカム変数と 1 つ以上の予測変数の間の関係を定量化するために使用される一般的な分析手法です。 アウトカム変数は従属変数と呼ばれることが多く、予測変数は独立変数と呼ばれることがよくあります。 予測変数は、バイナリ、カテゴリ、または連続のいずれかです。 ここでは、Stata の regress コマンドを使用して単回帰モデルを当てはめる方法を学び、後でより高度な機能を検討します。
まず、データセット nhanes2l を開いてみましょう。
. webuse nhanes2l
単回帰分析は、2 つの連続変数間の線形関係を調査するためによく使用されます。 線形回帰モデルを当てはめる前に、散布図を作成して変数間の関係を調べると便利です。 体格指数 (bmi) と年齢(age)の散布図を作成してみましょう。
. twoway (scatter bmi age)
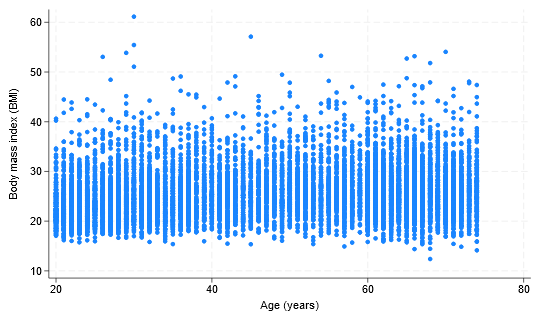
散布図はわずかな上昇傾向を示しており、 age の値が大きいほど bmi の値が大きくなります。
線形回帰を使用して、散布図内の点群を最もよく表す直線を特定します。 「最もよく表される」とは、各観測値と線の間の垂直方向の差の二乗和が最小となる線として定義されます。 直線は以下の方程式で定義され、データを使用して切片と傾きを推定します。
bmi = 切片 + 傾き * age
regress に続いてアウトカム変数 bmi 、さらに続けて予測変数 age を入力して、切片と傾きを推定しましょう。
. regress bmi age
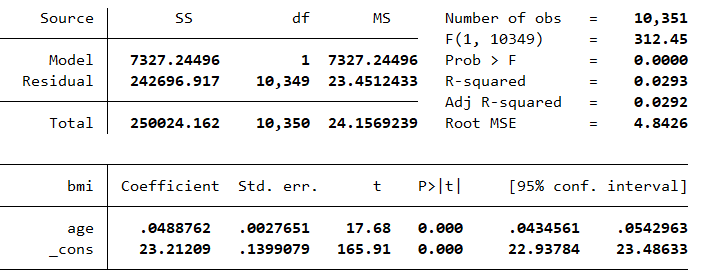
切片は「_cons」というラベルの付いた係数で示され、傾きは「age」というラベルの付いた係数です。
generate コマンドを使用して bmi_predicted という名前の新しい変数を作成しましょう。 これは、出力からの切片と傾きを使用して回帰直線を定義します。
. generate double bmi_predicted = 23.21209 + 0.0488762 * age
次に、twoway line コマンドを使用して、散布図で回帰直線をプロットしましょう。
. twoway (scatter bmi age) (line bmi_predicted age)
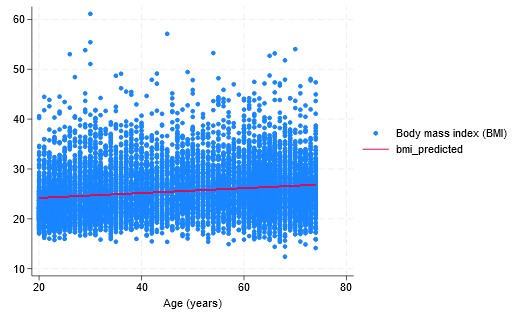
回帰直線はわずかに上向きの傾きを持っており、これは、age の値が大きいほど、bmi の値が大きい傾向があることを示唆しています。 この傾きから、年齢が 1 歳増えるごとに BMI が 0.049 増加することがわかります。 推定した age の係数の p 値には「P>|t|」というラベルが付けられます。 そして、係数がゼロに等しい (関係なし) という帰無仮説を検定します。 p 値は 0.000 に等しく、この結果は age と bmi の間に関係がないという帰無仮説と矛盾していることを示唆しています。
これが線形回帰の基本的な考え方です。 ただし、出力された表には他にも多くの数値があり、「帰無仮説」という用語も定義せずに使用しています。 それが何を意味するのかを知るために、もう少し深く掘り下げてみましょう。
さらに詳しく確認しよう
まず、帰無仮説と対立仮説を定義しましょう。 私たちの帰無仮説は、age と bmi の間には関係がなく、回帰直線は平坦であるというものです。 言い換えれば、bmi の最良の予測は、単に年齢の値ごとの BMI の平均値です。 egen と twoway line コマンドを使用して、BMI の平均値の平らな線を引いてみましょう。
. egen double bmi_mean = mean(bmi). twoway (scatter bmi age) (line bmi_predicted age) (line bmi_mean age)
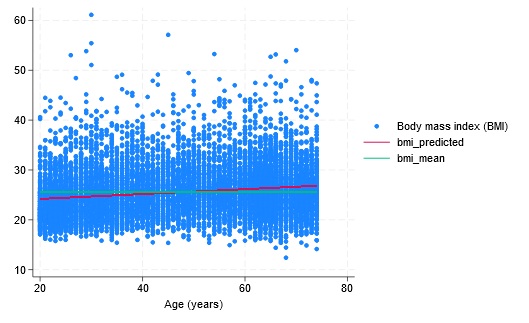
私たちの対立仮説は、age と bmi の間には関係があり、回帰直線はグラフの赤い線のように平らではないというものです。
「赤い線は本当に緑の線と違うのか?」と自問するかもしれません。 または、「回帰直線の傾きは、age と bmi の間の意味のある関係を説明するのに十分な大きさでしょうか? それとも、回帰直線は基本的に平坦ですか?」 これらの質問に答えるために p 値を使用しましたが、p 値はどこから来たのでしょうか?
この質問には、regress コマンドの出力を使用して答えることができます。 出力には、3 つのグループに分けられて複数の数値が表示されています。 左上の最初のグループは「ANOVA テーブル」と呼ばれることが多く、ANOVA は「ANalogy Of VAriance」の略です。 右上の 2 番目のグループには、モデル全体に関する情報が表示されます。 一番下の 3 番目のグループには、各予測変数とアウトカム変数の関係に関する情報が表示されます。
分散分析表( ANOVA テーブル)
ANOVA テーブルには、「SS」、「df」、「MS」というラベルの付いた列があり、それぞれ「平方和」、「自由度」、「平均平方」を表します。 「Source」というラベルの付いた最初の列には、「Model」、「Residual」、「Total」というラベルの付いた行があります。 数値の意味を理解するために、表の数字を手動で計算してみましょう。
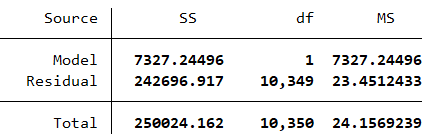
「Total」行の「SS」は 250,024.162 に相当し、これを「全変動」と呼びます。 これは、グラフ内の各青い点と緑の線の間の垂直距離の 2 乗を合計することによって計算されます。 これは、帰無仮説が真であると仮定して、bmi の観察値が予測した bmi からどの程度乖離しているかを定量化します。
. generate double ss_total = (bmi - bmi_mean)^2. table, statistic(total ss_total) nformat(%16.3f total)
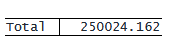
丸め誤差のため、計算はわずかに異なります。 Stata の回帰コマンドは、単純な計算よりもはるかに正確なアルゴリズムを使用します。 しかし、考え方は同じです。
次に、「Residual」行の「SS」の値を計算してみましょう。これは 242,696.917 に相当します。 これは、グラフ内の各青い点と赤い線の間の垂直距離の 2 乗を合計することによって計算されます。 これは、対立仮説が真であると仮定して、bmi の観察値が bmi の予測値からどの程度乖離しているかを定量化します。
. generate double ss_residual = (bmi - bmi_predicted)^2. table, statistic(total ss_residual) nformat(%16.3f total)
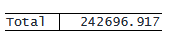
最後に、「Model」行の「SS」の値を計算してみましょう。これは 7,327.24 に相当します。 これは、グラフ内の各青い点の赤い線と緑の線の間の垂直距離の 2 乗を合計することによって計算されます。 対立仮説が正しいと仮定した場合と帰無仮説が正しいと仮定した場合に、bmi の予測値がそれぞれどの程度乖離しているかを定量化します。
. generate double ss_model = (bmi_predicted - bmi_mean)^2. table, statistic(total ss_model) nformat(%16.3f total)
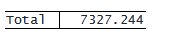
ss_model と ss_residual の合計は常に ss_total と等しいことに注意してください。
. table, statistic(total ss_model ss_residual ss_total) nformat(%16.3f total)
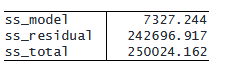
ANOVA テーブルの df 列には、自由度が表示されます。 モデルの df は、推定パラメータの数 k から 1 を引いたものと等しくなります。 切片と age 傾きを推定したため、k - 1 = 2 - 1 = 1 となります。 残差の df は、サンプルサイズ n から推定パラメーターの数 k を引いたものと等しくなります。 サンプルサイズは 10,351 で、2 つのパラメーターを推定したため、n - k = 10,351 - 2 = 10,349 となります。 合計の df は、サンプルサイズ n から 1 を引いたものと等しくなります。 この例では、n - 1 = 10,351 - 1 = 10,350 となります。
MS 列には、「平均平方」が表示されます。 MS は SS を df で割った値に等しくなります。 これは display コマンドを使用して確認できます。
. display "Model MS = " 7327.24496 / 1
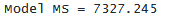
. display "Residual MS = " 242696.917 / 10349
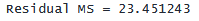
. display "Total MS = " 250024.162 / 10350
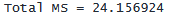
手作業で計算を行うと多少の丸め誤差が生じますが、数値は基本的に回帰の出力と同じです。
モデル統計
出力結果の右上にある 2 番目の数値グループには、モデルに関する情報が表示されます。 「Number of obs.」は Stata がモデルを当てはめるために 10,351 個の観測行を使用したことがわかります。

次の行「F(1, 10349)」は F 統計量です。 F 統計量はモデルの平均平方と残差の比率であり、この例では 7327.24 / 23.45 = 312.45 です。 括弧内の数字はそれぞれ分子と分母の自由度であり、分散分析表にも示されています。 F 統計量の値には直接的な解釈はありませんが、それを使用して「Prob > F」というラベルの付いた p 値を計算できます。 Stata の Ftail() 関数を使用して p 値を手動で計算できます。
. display "Prob > F = " Ftail(1, 10349, 312.45)
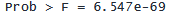
結果の 6.547e-69 は、本質的にゼロである非常に小さな数です。 p 値は、モデル内のすべての傾き係数 (切片は除く) が同時に 0 に等しいという帰無仮説を検定するために使用されます。 p 値が小さいことは、結果が age の係数が 0 であるという帰無仮説と矛盾していることを示唆しています。 別の解釈としては、私たちのモデルは切片のみを含むモデルよりもデータによく適合するということです。
回帰モデルの残差は正規分布する必要があるという話をよく聞きます。 統計理論によれば、平均がゼロの正規分布変数の二乗は中心 χ2 分布を持ちます。 また、2 つの独立した χ2 をそれぞれの自由度で割った比が F 分布になることもわかります。 正規分布に従う残差を二乗して平方和を計算し、平方和を自由度で割って平均平方を算出し、平均平方の比をとって F 統計量を取得できます。 「残差の正規性」の仮定により、F 分布を使用して F 統計量の p 値を計算できます。
表の次の数値には「R-squared」というラベルが付いています。 R2 は Model の平方和と Total の平方和の比率です。 display コマンドを使用して R2 を手動で計算できます。
. display "R-squared = " 7327.24496 / 250024.162
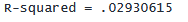
R2 は、モデルによって説明されるアウトカム変数の変動の割合として解釈されることがよくあります。 この解釈を使用すると、私たちのモデルは bmi の変動の 2.9% を説明します。
次の数値は「Adj R-squared」というラベルが付けられており、R2 と似ています。
ただし、モデル内の不必要な可能性のある変数を考慮するために、ペナルティが課されます。
「Root MSE」とラベル付けされた次の数値は、残差の平均平方の平方根です。 これを手動で確認してみましょう。
. display "Root MSE = " sqrt(23.4512433)
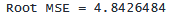
Root MSE は、bmi の観察値が回帰直線から平均 4.84 ポイント外れていることを示します。
回帰統計
出力結果の下部にある 3 番目の数値グループには、各予測変数とアウトカム変数の間の関係に関する情報が表示されます。 「_cons」というラベルの付いた行は切片について示していますが、通常は傾きに注目します。

「係数」というラベルの付いた列には、モデル内の各変数の推定された傾きが表示されます。 age の係数は 0.0488762 であり、上で述べたように、 これは年齢が 1 増えるごとに BMI が 0.049 増加することを意味すると解釈します。
Stata は係数の標準誤差も推定し、それが「Std. err.」というラベルの付いた列に表示されます。 標準誤差の推定にはさまざまな方法が使用できますが、それらについては後で説明します。 Stata は、デフォルトで通常の最小二乗法を使用して標準誤差を推定します。
「t」というラベルが付いている次の列は t 統計量で、係数がゼロに等しいという帰無仮説を検定するために使用されます。 t 統計量は、推定された係数と帰無仮説 (ゼロ) を仮定した係数の値との差を標準誤差で割ったものです。 帰無仮説で仮定した係数は常にゼロであるため、通常は推定された係数を標準誤差で除算するだけです。
. display "t = " (0.0488762 - 0) / .0027651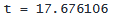
. display "t = " 0.0488762 / .0027651
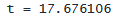
「P>|t|」というラベルが付いた次の列は、t 統計量の p 値です。 Stata の ttail() 関数を使用して p 値を計算できます。 ttail() 関数の最初の引数は自由度で、n - 1 = 10,351 - 1 = 10,350 です。 2 番目の引数は、t 統計量の絶対値です。 abs() 関数を使用して絶対値を計算できます。 両側の p 値を計算しているため、結果を 2 倍する必要があります。
. display "P>|t| = " 2*ttail(10350, abs(17.68))
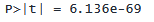
結果は、やはり、事実上ゼロである非常に小さな数値になります。 これは、係数がゼロに等しいという帰無仮説を棄却する必要があることを示唆しています。
次の 2 つの列「95% conf. interval」は、95% 信頼区間の下限と上限です。 数値の理解のために手動で計算してみましょう。 有意水準 0.05 の両側仮説検定に対応する t 分布の「臨界値」が必要になります。 Stata の invt() 関数を使用してこの数値を計算できます。 最初の引数は自由度で、n - 1 = 10,351 - 1 = 10,350 です。 2 番目の引数は 1 - alpha/2 = 1 - 0.05/2 = 0.975 です。 この数値に標準誤差を乗算し、係数から減算して下限を推定します。
. display "Lower 95% CI bound = " .0488762 - invt(10350, 0.975) * .0027651

臨界値に標準誤差を乗算し、それを係数に加えて上限を推定します。
. display "Upper 95% CI bound = " .0488762 + invt(10350, 0.975) * .0027651

95% 信頼区間を「信頼性」という言葉を使って解釈してしまいがちですが、それは正しくありません。 この間隔は、多くのサンプルから推定された間隔には、95% の確率で真の母集団パラメータが含まれるということを単純に示しています。
出力の数値とその計算方法を理解したところで、回帰モデルの結果を解釈してみましょう。
モデルの解釈
私たちのモデルは、アウトカム変数 bmi と予測変数 age の間の関係を調べました。 このモデルには 10,351 の観測行が使用されており、bmi の変動の約 3% が説明され、切片のみを含むモデルよりもデータによく適合します (F(1, 10349) = 312.45、p < 0.000)。 この結果は、年齢が 1 歳増えるごとに bmi が 0.049 増加することを示唆しています (t = 17.68、df = 10,350、p < 0.000)。
他にも回帰で使用できるオプションが多数あり、それらについてはマニュアルを参照してください。
参考
さらに詳しい内容につきましては、下記のマニュアルをご覧ください。


