EViews8

計量経済学と統計学に関する新機能:推定

推定に関する機能としてスイッチング回帰(外生/マルコフ)、ベイジアンVAR(BVAR)、堅牢な最小二乗法、ブレークポイント回帰、ヘックマンの選択モデルそしてパネル共和分推定をサポートしました。

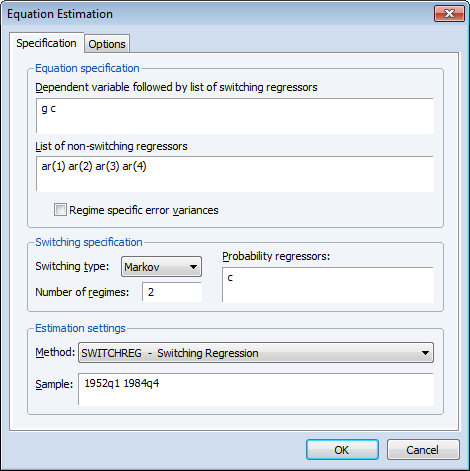
スイッチング回帰

EViews 8は一推定式によるスイッチング回帰モデルをサポートしました。レジーム間で離散的に変化する状態変数による非線形性に対応し、独立及びマルコフ過程の選択も行えます。また、スッチング回帰においてフィルタリング、平滑化、推定値による予測を行うツールも用意しています。

ダイナミクスをモデル化できるよう、ラグ付き被説明変数を説明変数としたり、自己相関のある誤差をモデルで利用することも可能です(Goldfeld and Quandt,1973,1976;Maddala,1986;Hamilton,1994;Fruhwirth-Schnatter,2006)。

switch

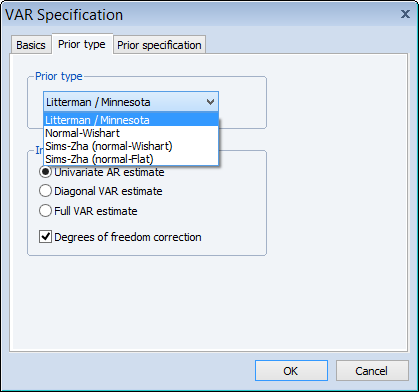
ベイジアンVAR

EViews 8は新たにベイジアンVARモデルの推定をサポートしました。その名が示すようにベイズ推定の手法を用いてVARモデルを推定します。EViewsがサポートしている事前分布を以下に示します。

Litterman/Minnesota事前分布
Normal-Wishart事前分布
Sims-Zha Normal-Wishart事前分布
Sims-Zha Normal-flat事前分布

BVARは無制約のVARモデル推定に比べ、シュリンケージという考え方を用いて推定するパラメータセットの総数を少なくします。

bvar

堅牢な最小二乗法

EViews 8は外れ値に対して堅牢な推定値を提供する堅牢な最小二乗法推定をサポートしました。EViewsのサポートしている手法は次の3つです：M-推定(Huber,1973),S-推定(Rousseeuw and Yohai,1984),MM-推定(Yohai 1987)。

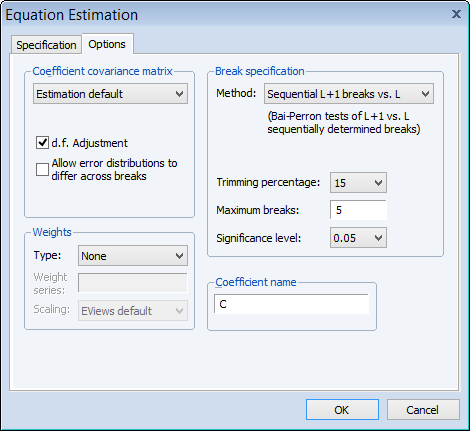
ブレークポイント回帰

EViews 8は構造変化に対応した線形回帰モデルを推定する新機能をサポートしました。レジームのブレークポイントが既知の場合だけでなく、未知の場合はBai(1997)、Bai and Perron (1998)によるグローバルマキシマイザ、連続法などを用いて推定を行います。ブレークポイントの推定においては全てのリグレッサが変化する場合、または、一部のリグレッサだけが変化する場合でも推定できます。

breakls

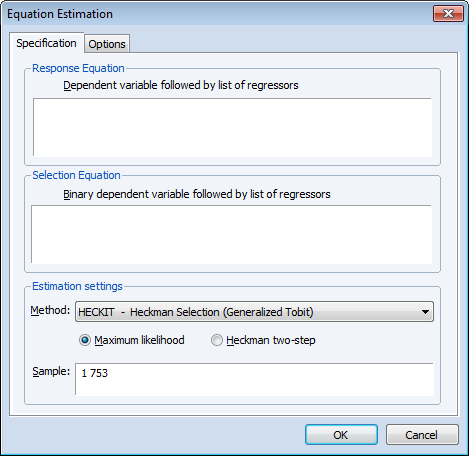
ヘックマンの選択モデル

ヘックマンの選択モデルのフレームワークは被説明変数yiはデータの一部である観測データに対する線形モデルである、とするものです。古典的な例として、よく利用されるものに女性の賃金推定式の問題があります。賃金は働くという意思決定を行った女性からのみ観測できます。その意思決定を行っていない女性のデータは観測できません。したがって、観測データから得られた推定値にはバイアスが生じており、適正なものとは言えません。

EViews 8はHeckman(1979)による推定量に対して2つの推定手法を提供しています。一つはヘックマンのオリジナルである2ステップ法、もう一つは最尤法推定を利用するものです。

heckman

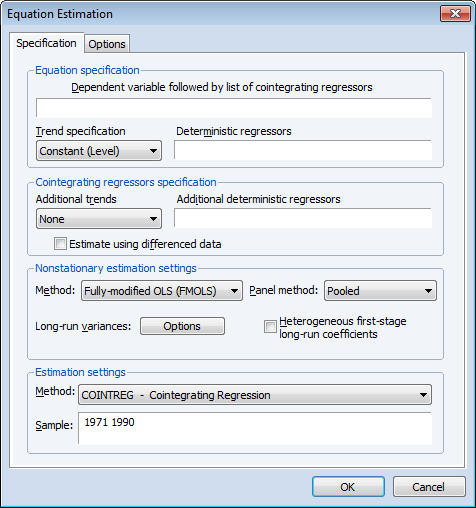
パネル共和分推定

EViews 8は一推定式によるパネル共和分推定のツールをサポートしています。Pedroni(2000)によるFully Modified OLS (FMOLS)パネル推定、Kao and Chiang(2000)、Mark and Sul(2003)によるパネルダイナミック最小二乗法(DOLS)推定をサポートしました。

どちらの推定量の場合でも、これらは推定値をクロスセクション単位で組み合わせたプール型および加重型をサポートしています。

pancoint

ユーザ定義の最適化

EViewsにはEquation, System, Sspace, VARなどの各オブジェクトにおいて最適化を用いた様々な推定手法が組み込まれています。

また、EViewsのログエル(logl)オブジェクトを利用すれば、ユーザ定義の尤度を最大化して推定値を求めることができます。ただし、旧バージョンまでは、利用できるのは観測値の入ったシリーズオブジェクトに限定されていました。

それに対し、EViews 8ではユーザ定義関数に対して最適なパラメータやコントロール値を計算する最適化コマンドを用意しました。この機能によりシリーズオブジェクトを使わずとも最適化計算ができるようになりました。