Sample Scripts from GB Books
GB012: 2次元の粘性流体

5. 側溝のあるチャネルにおける流れ

今度はチャネル右岸に矩形の凸部がある場合の流れについて解析してみます。基本的にはCase4のスクリプトを踏襲します。Cの値としてはここでも 1e3 を用いることにします。

5.1 Problem descriptor [ vfluid01e.pde ]

まずタイトルを設定します。
TITLE
'Channel with a Lateral Cavity' { vfluid01e.pde }

次に演算精度に関するセレクタをセットします。Errlim = 1e-3 という設定では解への収束が見られないため、若干演算精度を落として計算を実行します。
SELECT
Errlim = 3*1e-3

従属変数を定義します。
VARIABLES
    vx
    vy
    p

関連するパラメータや数式を定義します。nx, ny の算出式については gb012c を参照ください。
DEFINITIONS
    Lx = 1.0 Ly = 1.0
    visc = 0.1                    { Viscosity }
    delp = 1e-6                   { Driving pressure }
    dens = 1e3                    { Mass density }
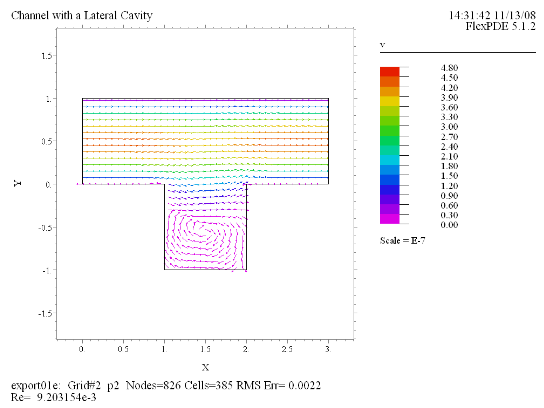
    Re = dens*globalmax(vx)*2*Ly/visc      { Reynolds number }
    v = vector(vx, vy) vm = magnitude(v) { Speed }
    unit_x = vector(1, 0)         { Unit vector fields }
    unit_y = vector(0, 1)
    nx = normal(unit_x)           { Direction cosines }
    ny = normal(unit_y)
    natp = visc*(nx*div(grad(vx)) + ny*div(grad(vy)))
                                  { Natural boundary condition for p }
    C = 1e3

方程式を定義します。
EQUATIONS
    vx: dx(p) - visc*div(grad(vx)) = 0
    vy: dy(p) - visc*div(grad(vy)) = 0
    p:   div(grad(p)) - C*visc/Ly^2*div(v) = 0

BOUNDARIESセクションでは境界形状の規定と同時に境界条件を設定します。
BOUNDARIES
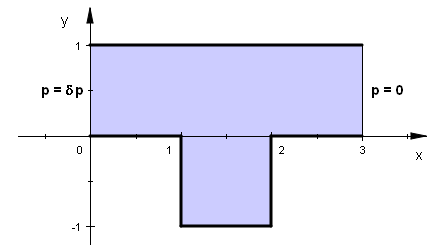
    Region 1
      Start 'outer' (0, Ly)
        Natural(vx) = 0 Value(vy) = 0 Value(p) = delp    { In }
          Line to (0, 0)
        Value(vx) = 0 Value(vy) = 0 Natural(p) = natp    { Lower }
          Line to (Lx, 0) to (Lx, -Ly) to (2*Lx, -Ly)
               to (2*Lx, 0) to (3*Lx, 0)
        Natural(vx) = 0 Value(p) = 0                     { Out }
          Line to (3*Lx, Ly)
        Value(vx) = 0 Value(vy) = 0 Natural(p) = natp    { Upper }
          Line to Close

最後に出力すべき情報を規定します。
PLOTS
    Grid(x, y)
    Vector(v) norm Report(Re)
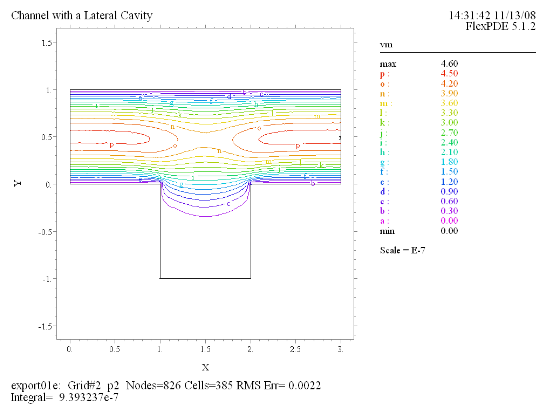
    Contour(vm)
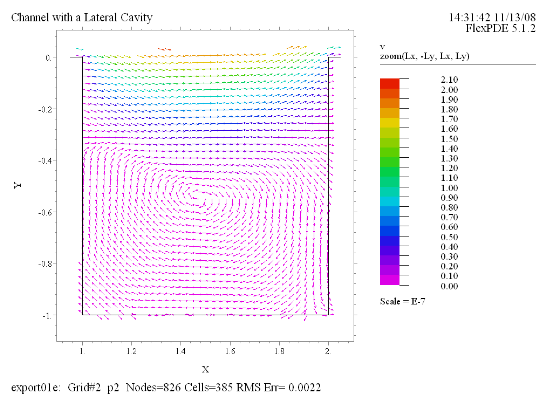
    Vector(v) norm zoom(Lx, -Ly, Lx, Ly)
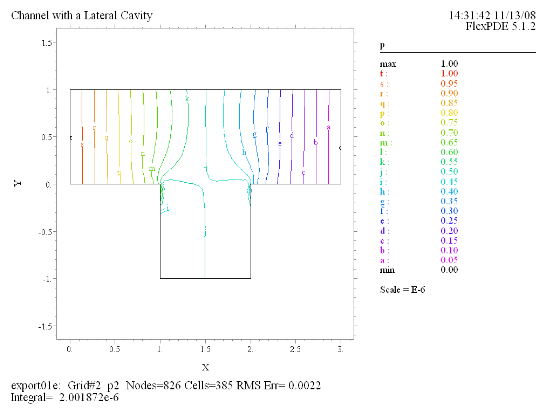
    Contour(p)
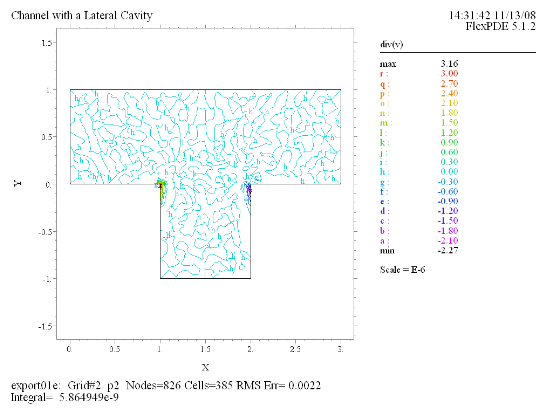
    Contour(div(v))
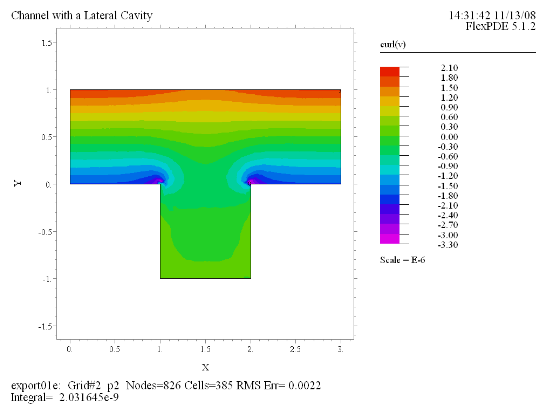
    Contour(curl(v)) painted

END