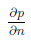Sample Scripts from GB Books
GB012: 2次元の粘性流体
4. くびれのあるチャネルにおける流れ [2]
|
4.1 Problem descriptor [ vfluid01d.pde ]
前ケースのスクリプト vfluid01c.pde に対する変分のみを記すことにします。 PLOTSセクションに対しては次の変更を加えます。最後の1文は追加です。 |
4.2 実行結果
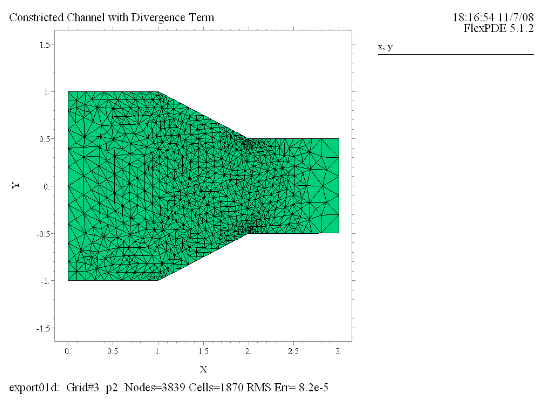
(1) Grid(x, y) |
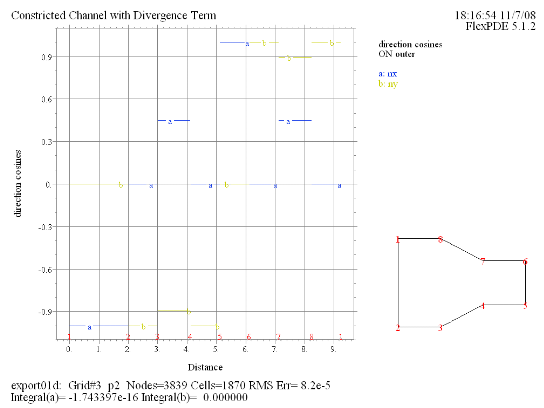
(2) Elevation(nx, ny) on 'outer' as 'direction cosines' |
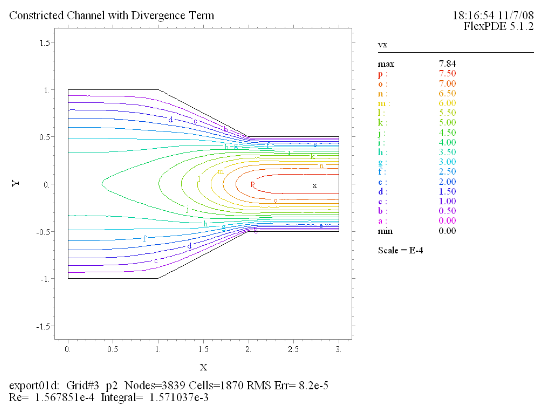
(3) Contour(vx) Report(Re) |
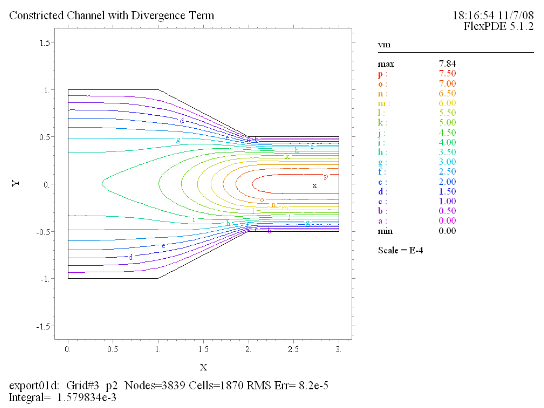
(4) Contour(vm) |
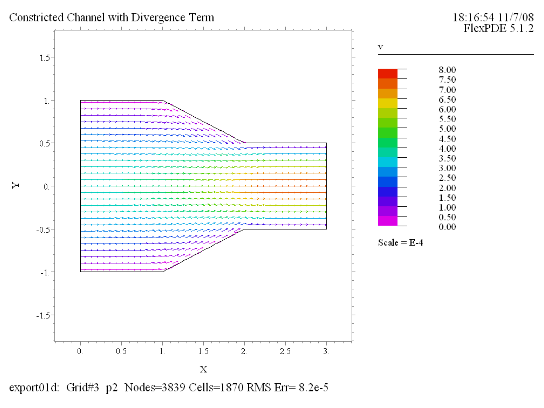
(5) Vector(v) norm |
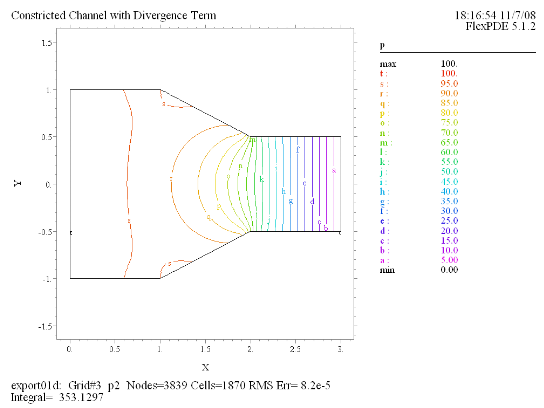
(6) Contour(p) |
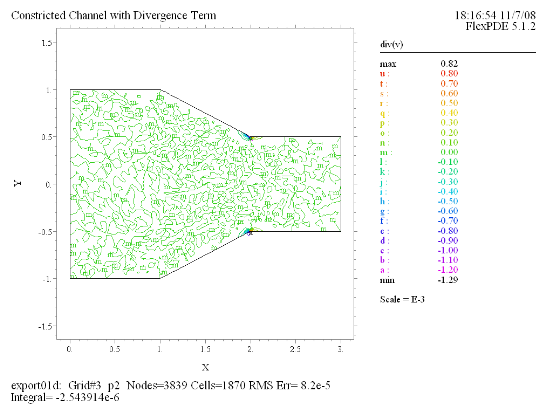
(7) Contour(div(v)) |
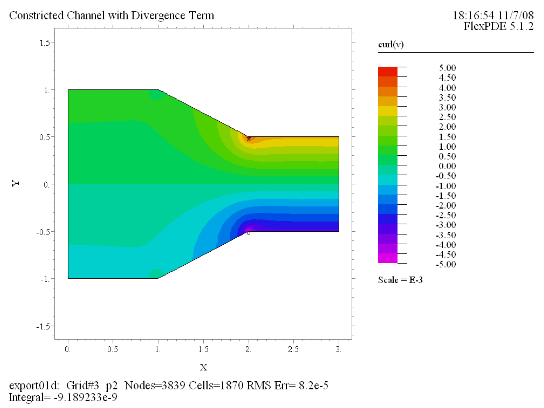
(8) Contour(curl(v)) painted |
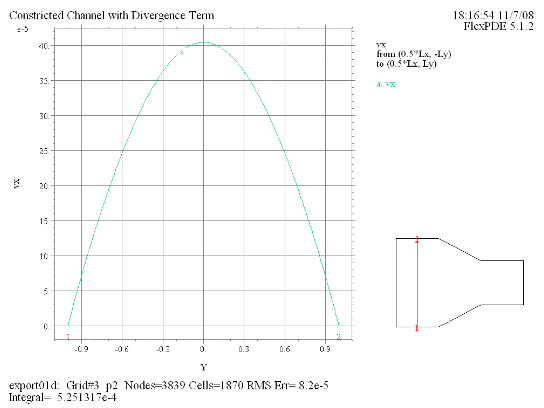
(9) Elevation(vx) from (0.5*Lx, -Ly) to (0.5*Lx, Ly) |
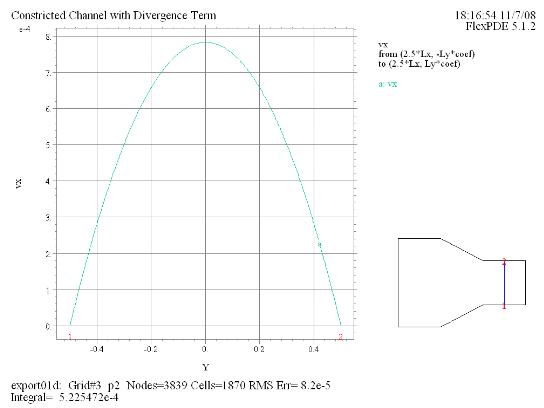
(10) Elevation(vx) from (2.5*Lx, -Ly*coef) to (2.5*Lx, Ly*coef) |
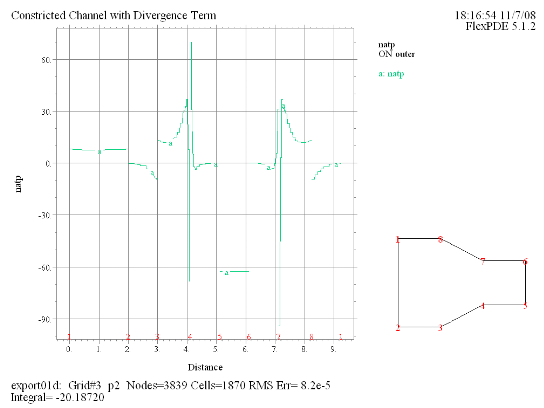
(11) Elevation(natp) on 'outer' |

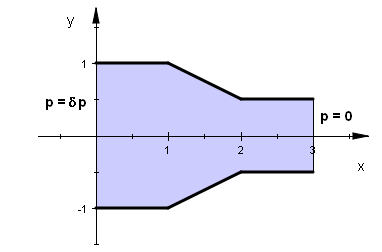 前ケースと全く同じ問題ですが、今回は
div(v) が 0 となるような解を誘導すべく、数式(13)(資料
前ケースと全く同じ問題ですが、今回は
div(v) が 0 となるような解を誘導すべく、数式(13)(資料