Sample Scripts from GB Books
GB012: 2次元の粘性流体
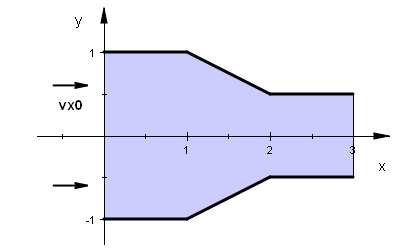
6. くびれのあるチャネルにおける流れ [3]
Case3, 4ではチャネル入口部において一定の圧力をかけた場合を想定し解析を行いましたが、ここでは流速値が一定という条件を課したときの流れについて計算を行ってみます。 |
6.1 Problem descriptor [ vfluid01f.pde ]
まずタイトルを設定します。 従属変数を規定します。 関連するパラメータや数式を定義します。Case3,
4の場合とは全く異なる粘性係数値が使用されている点に注意してください。vx0
の値はReynolds数が小さな値を取るように考慮して設定する必要があります。Cの値は条件に合わせて試行錯誤が必要です。 方程式を定義します。 BOUNDARIESセクションでは境界形状の規定と同時に境界条件を設定します。
圧力 p については基本的にその微分値(自然境界条件)で規定しますが、出口部についてはDirichlet型で p = 0
という指定を行っています。現実の圧力という意味では得られた p の値に大気圧を加える必要があります。 最後に出力すべき情報を規定します。 |
6.2 実行結果
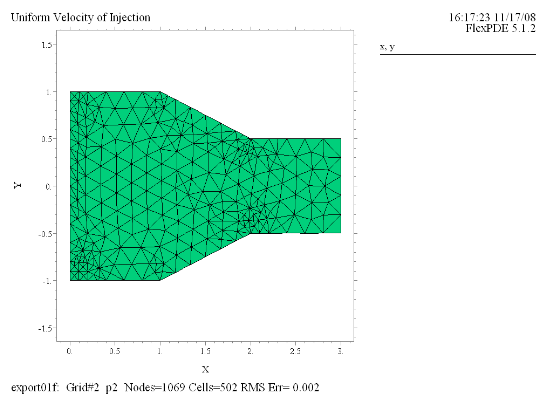
(1) Grid(x, y) |
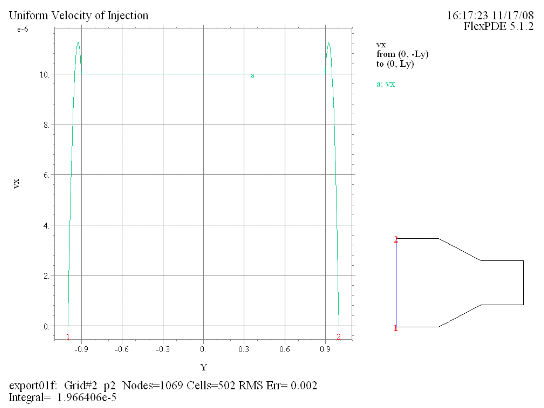
(2) Elevation(vx) from (0, -Ly) to (0, Ly) |
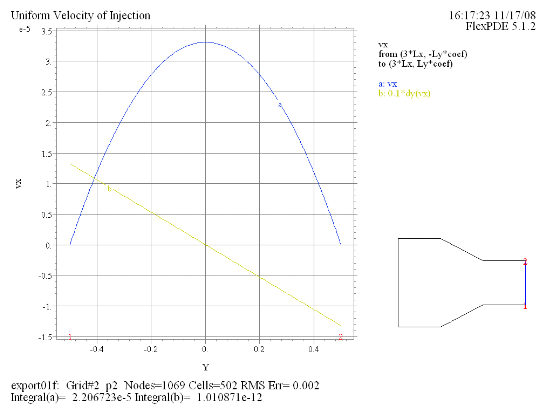
(3) Elevation(vx, 0.1*dy(vx)) from (3*Lx, -Ly*coef) to (3*Lx, Ly*coef) |
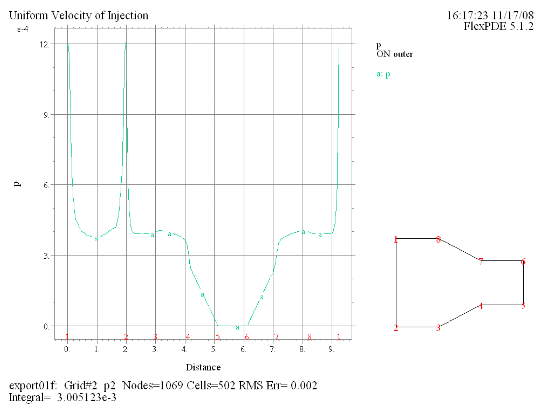
(4) Elevation(p) on 'outer' |
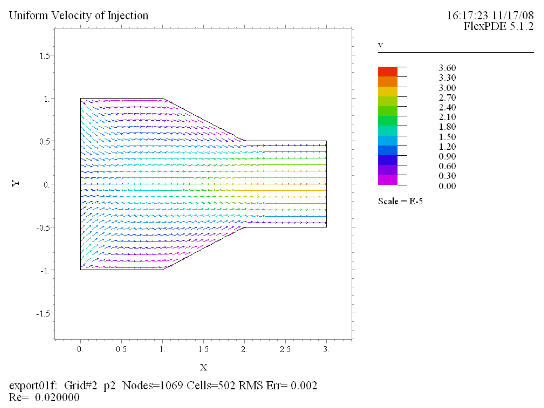
(5) Vector(v) norm Report(Re) |
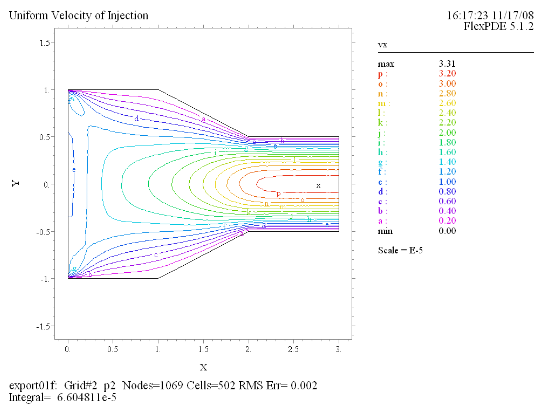
(6) Contour(vx) |
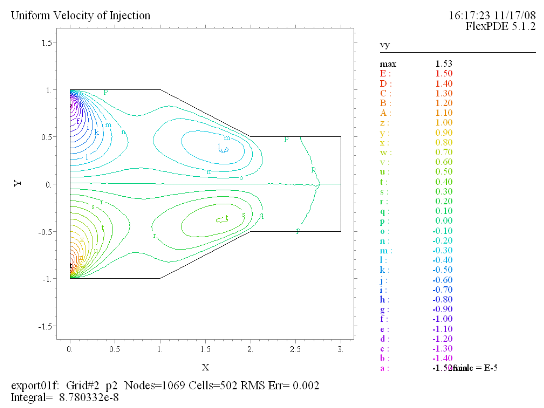
(7) Contour(vy) |
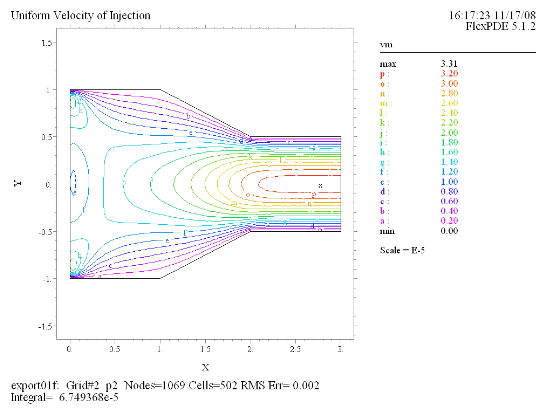
(8) Contour(vm) |
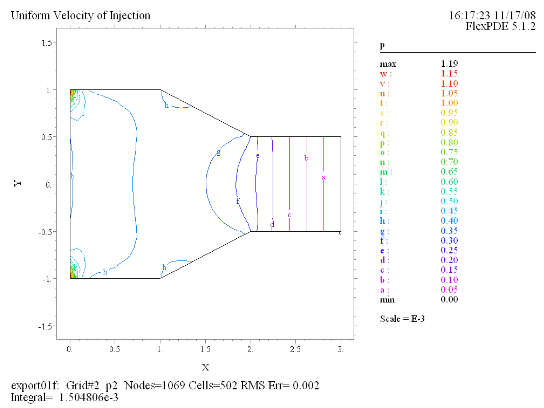
(9) Contour(p) |
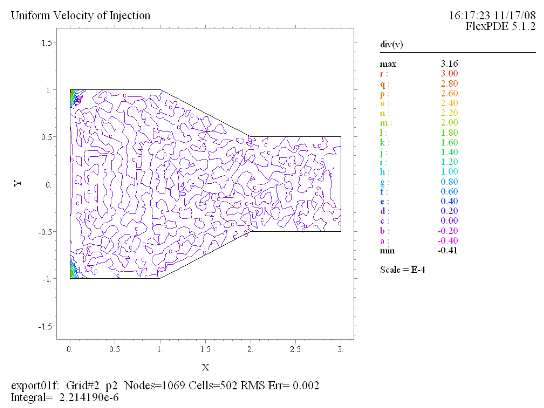
(10) Contour(div(v)) |
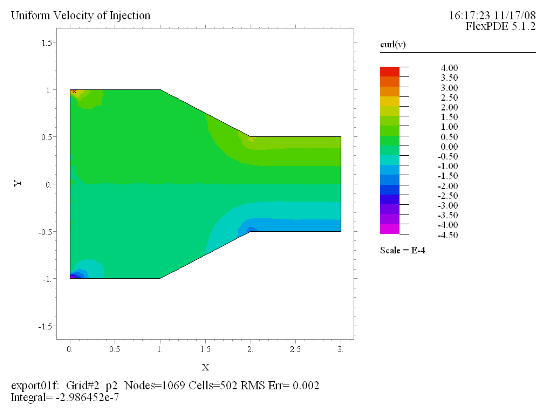
(11) Contour(curl(v)) painted |