まずタイトルを設定します。
TITLE
'Glass Block in a Parallel Field' {
3dfields1e.pde }
次に演算精度に関するセレクタをセットします。
SELECT
Errlim = 1e-4
座標系が3次元直交座標系であることを明示します(デフォルトはCartesian2)。
COORDINATES
Cartesian3
従属変数を定義します。
VARIABLES
U
偏微分方程式の定義に先立ち、パラメータ類 や関係式を定義します。なお、permittivityは誘電率、dielectric
displacementは誘電変位、あるいは電束密度を表す英語です。
DEFINITIONS
L = 1.0 Lx = 0.1 Ly = 0.05 Lz = 0.03
eps0 = 8.854e-12
{ Permittivity of vacuum }
epsr
{ Relative permittivity }
eps = epsr*eps0
{ Permittivity }
E0 = 1.0 D_0 = eps0*E0
{ Far field }
E = -grad(U) Em = magnitude(E)
D = eps*E Dm = magnitude(D) {
Dielectric displacement }
誘電体を対象とする場合の偏微分方程式を規定します。真電荷が存在しないケースなので右辺は 0 となります(GB007 参照)。
EQUATIONS
div(D) = 0
Extrusionの設定に際しては水平面のみを考えれば良いので話は単純です。なおレイヤの定義が必要になるのは空気とガラスとで誘電率が異なるためです。
EXTRUSION
{ Parallel surfaces }
Surface 'bottom' z = -L
Layer 'air 1'
{ Layer below block }
Surface 'lower' z = -Lz
{ Lower face of block }
Layer 'glass'
{ Layer containing glass }
Surface 'upper' z = Lz
{ Upper face of block }
Layer 'air 2'
{ Layer above block }
Surface 'top' z = L
BOUNDARIESセクションにおいてbase
plane上でのリージョン構成定義と境界条件の設定を行います。平行場ということなので、まず上面と下面で自然境界条件型の指定を行います。
BOUNDARIES
Surface 'bottom' Natural(U) = D_0 { Since D=-eps*grad(U)
}
Surface 'top' Natural(U) = -D_0
次にbase
plane上でドメイン(この場合、正方形)の定義を行います。またそれがextrudeされた3次元領域内で設定されるべきパラメータ(この場合、比誘電率)を規定します。ただしガラスブロックの部分については次のリージョン定義で上書きされます。なお、この部分で Natural(U) = 0 という境界条件を指定していますが、これはextrudeされた周囲の側壁に対して適用されます。
Region 'domain'
{ Full solution domain }
Layer 'air 1' epsr = 1
Layer 'glass' epsr = 1
Layer 'air 2' epsr = 1
Start (-L, -L) Natural(U) = 0
Line to (L, -L) to (L, L) to (-L, L)
to Close
Base
plane上でガラスブロックに対応する長方形のリージョンを定義、それをextrudeした柱状領域でレイヤごとにパラメータ値を再設定します。
Region 'block'
{ Redefine space }
Layer 'air 1' epsr = 1
Layer 'glass' epsr = 7.0
{ Glass block }
Layer 'air 2' epsr = 1
Start (-Lx, -Ly) Line to (Lx, -Ly) to (Lx, Ly)
to (-Lx, Ly) to Close
最後に出力すべき情報を規定します。
PLOTS
Grid(x, y, z)
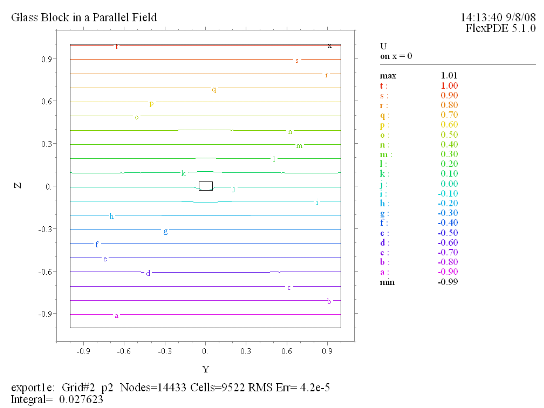
Contour(U) on x = 0
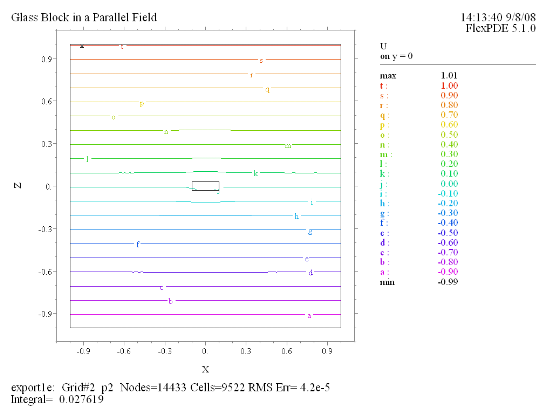
Contour(U) on y = 0
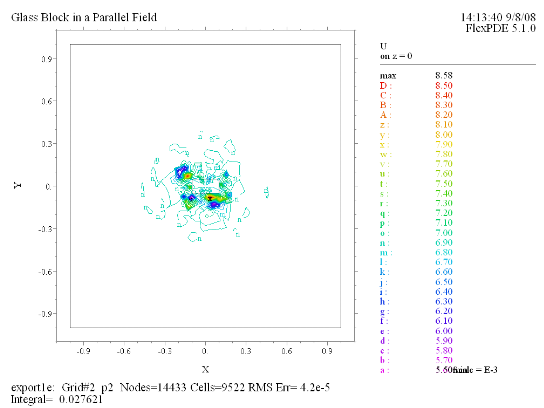
Contour(U) on z = 0
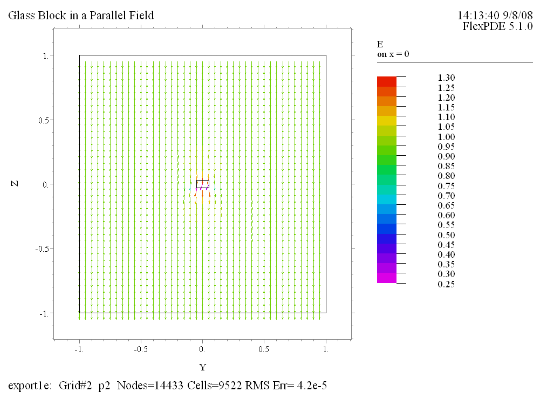
Vector(E) norm on x = 0
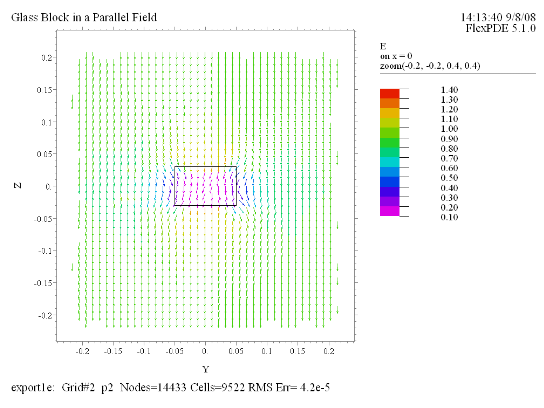
Vector(E) norm on x = 0 zoom(-0.2, -0.2, 0.4, 0.4)
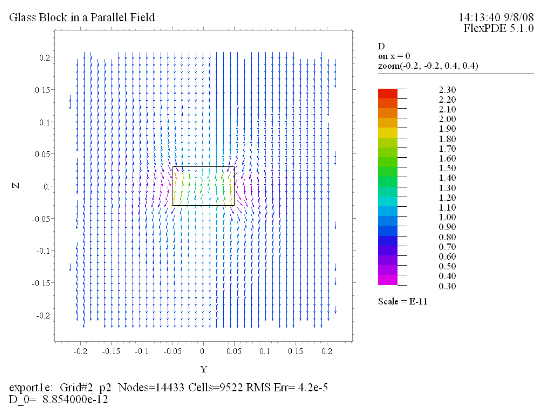
Vector(D) norm on x = 0 zoom(-0.2, -0.2, 0.4, 0.4)
Report(D_0)
END |

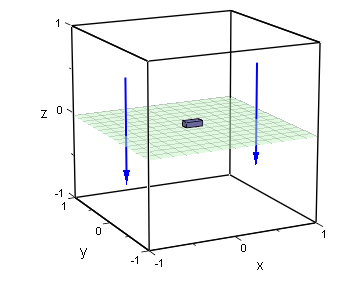 ここでは平行な電場中に直方体の形状のガラスが置かれていたときの場の様子をFlexPDEで解析してみます。
ここでは平行な電場中に直方体の形状のガラスが置かれていたときの場の様子をFlexPDEで解析してみます。