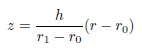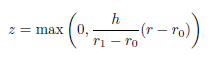Sample Scripts from GB Books
GB009: 3次元の電場
4. 円錐台中の電導
|
この場合も extrusion
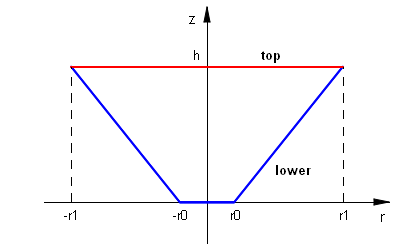
の考え方で3次元オブジェクトの定義を行うわけですが、その場合、下面lower(下図で青の部分)の設定が少々わかりにくいかも知れません。円柱座標系で動径の長さを
r としたとき、斜面を規定する方程式は |
4.1 Problem descriptor [ 3dfields1d.pde ]
まずタイトルを設定します。 座標系が3次元直交座標系であることを明示します(デフォルトはCartesian2)。 従属変数を定義します。 偏微分方程式の定義に先立ち、パラメータ類 や関係式を定義します。本ケースでは電流を伴うため、電流密度ベクトルJの規定が必要となります。
背景情報については GB003 を参照ください。 z軸方向へのextrusionを定義します。実際には下面と上面の定義があるのみなので、その間の空間の特性は一様となります。なお、面'lower'の定義文中で使われている rad というのはDEFINITIONSセクションで定義されている通り、円柱座標系での動径を意味します。 BOUNDARIESセクションにおいてbase
plane上でのリージョン構成定義と境界条件の設定を行います。Base
planeがこの場合平面ではないため、やや変則的です。また半径が r0 の円形リージョンを定義していますが、これは下面'lower'内でこの部分のみ境界条件が異なるためです。 最後に出力すべき情報を規定します。 |
4.2 実行結果
(1) Grid(x, y, z) Report(power) Report(current) |
(2) Contour(U) on x = 0 |
(3) Vector(J) norm on x = 0 |
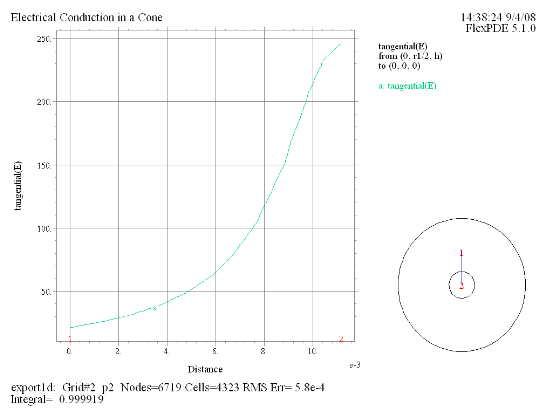
(4) Elevation(tangential(E)) |

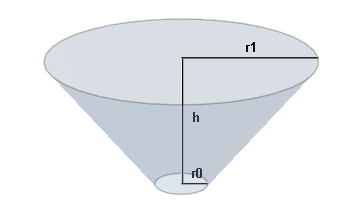 今度は
右図のような円錐台の形状をしたシリコン製の物体が与えられたとします。上面に 1V の電位をかけたときの電導の様子について、FlexPDEを用いて解析を行います。
その際、下面の電位は 0 に、周囲の斜面は絶縁状態に保たれているものとします。ただし、関連する寸法は次の通りです。
今度は
右図のような円錐台の形状をしたシリコン製の物体が与えられたとします。上面に 1V の電位をかけたときの電導の様子について、FlexPDEを用いて解析を行います。
その際、下面の電位は 0 に、周囲の斜面は絶縁状態に保たれているものとします。ただし、関連する寸法は次の通りです。