Sample Scripts from GB Books
GB003: 2次元における電導
6. 2種の金属からなる矩形プレート
|
6.1 Problem descriptor [ econduction01f.pde ]
TITLE |
6.2 実行結果
(1) Grid(x, y) |
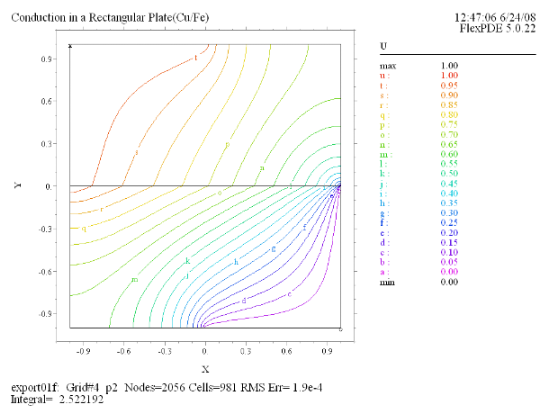
(2) Contour(U) |
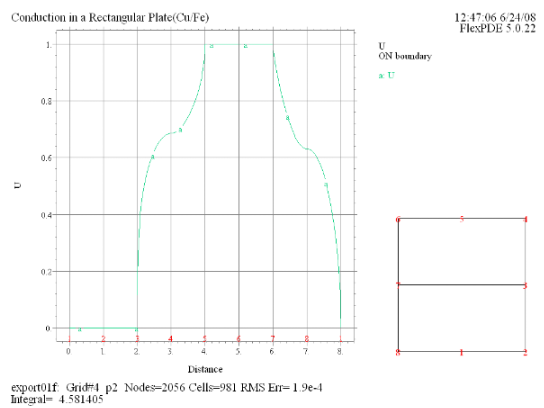
(3) Elevation(U) on
'boundary' |
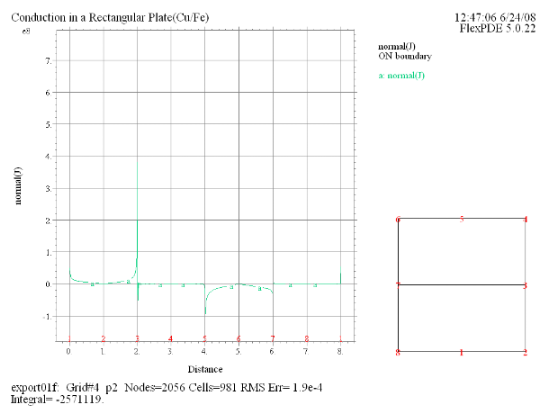
(4) Elevation(normal(J))
on 'boundary' |
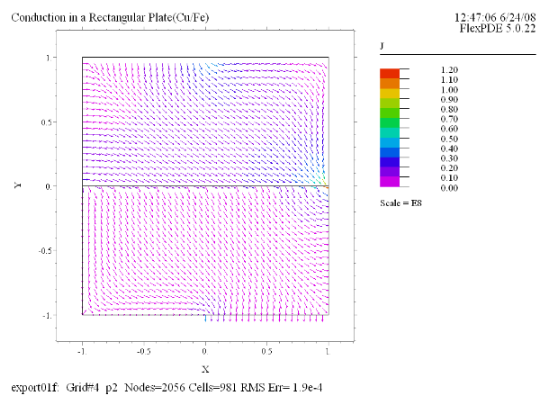
(5) Vector(J) norm |
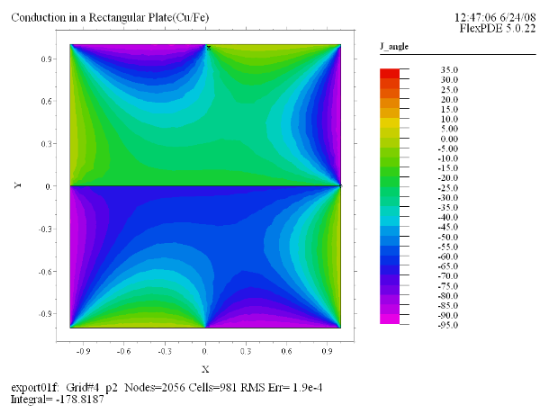
(6) Contour(J_angle)
painted |
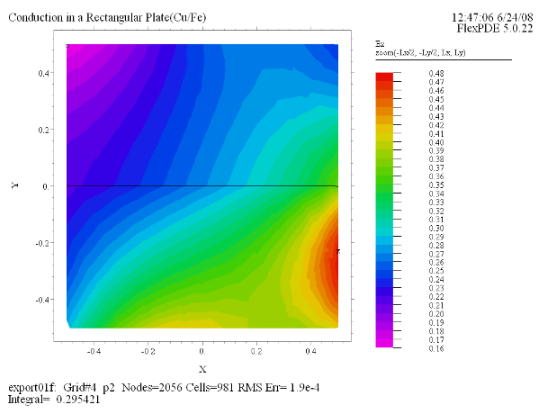
(7) Contour(Ex) painted
zoom(-Lx/2, -Ly/2, Lx, Ly) |
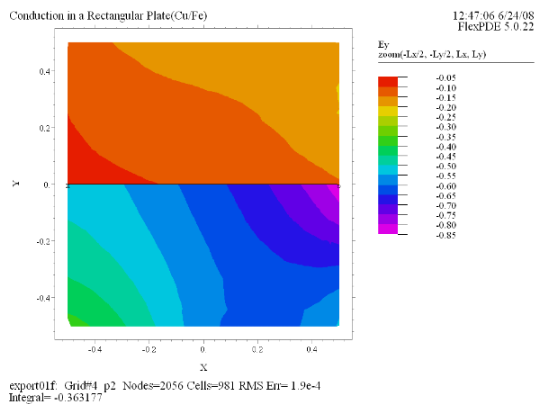
(8) Contour(Ey) painted
zoom(-Lx/2, -Ly/2, Lx, Ly) |
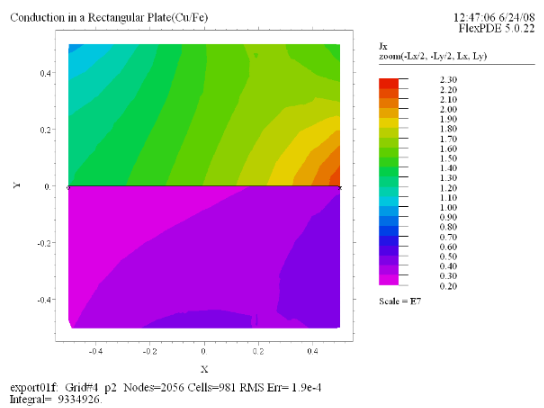
(9) Contour(Jx) painted
zoom(-Lx/2, -Ly/2, Lx, Ly) |
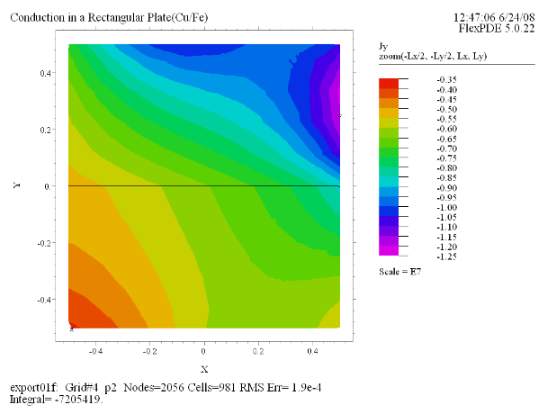
(10) Contour(Jy) painted
zoom(-Lx/2, -Ly/2, Lx, Ly) |
*1 Cheng, D. K. Field and Wave Electromagnetics, 2nd edn, Addison-Wesley, 1989 |

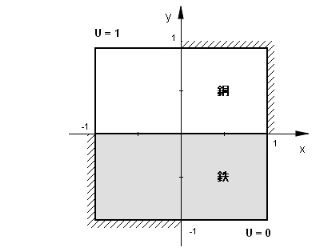 これまでは均一な材質からなるオブジェクトのみを扱ってきましたが、FlexPDEでは材質が連続的に変化する場合や不連続に変化する場合も容易に扱えます。ここでは右図に示すように上半分は銅、下半分は鉄からなる金属プレートを考えることにします。ハッチングを施した境界は絶縁されているとし、左上隅に
U = 1 の電位をかけ、右下隅の電位は U = 0 に保つものとします。このときの電導のパターンを調べてみましょう。
これまでは均一な材質からなるオブジェクトのみを扱ってきましたが、FlexPDEでは材質が連続的に変化する場合や不連続に変化する場合も容易に扱えます。ここでは右図に示すように上半分は銅、下半分は鉄からなる金属プレートを考えることにします。ハッチングを施した境界は絶縁されているとし、左上隅に
U = 1 の電位をかけ、右下隅の電位は U = 0 に保つものとします。このときの電導のパターンを調べてみましょう。