Sample Scripts from GB Books
GB003: 2次元における電導
5. くびれのある矩形プレート
|
5.1 Problem descriptor [ econduction01e.pde ]
TITLE |
5.2 実行結果
(1) Grid(x, y) |
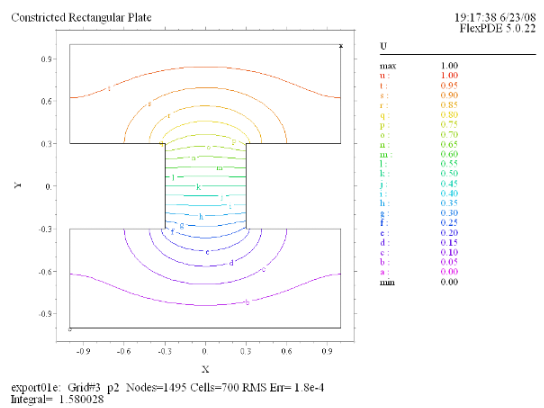
(2) Contour(U) |
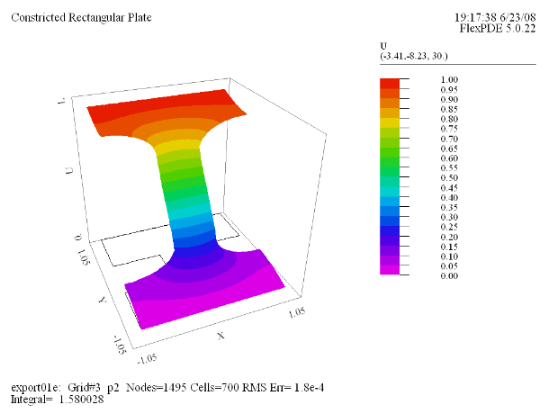
(3) Surface(U) |
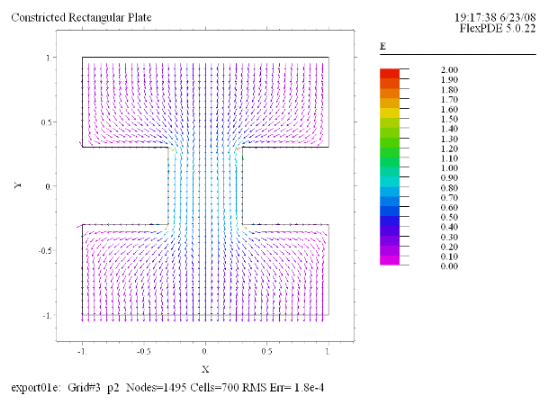
(4) Vector(E) norm |
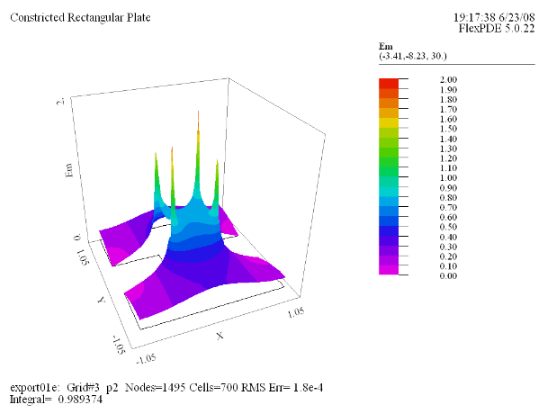
(5) Surface(Em) |
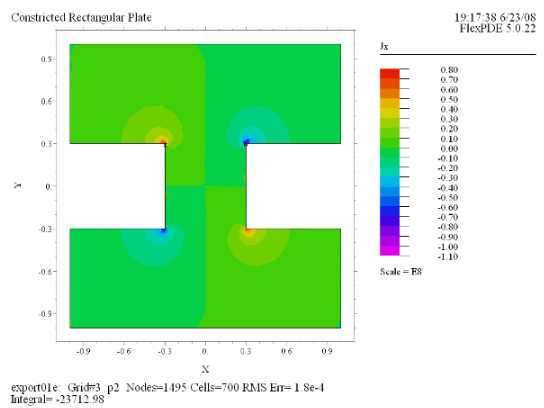
(6) Contour(Jx) painted |
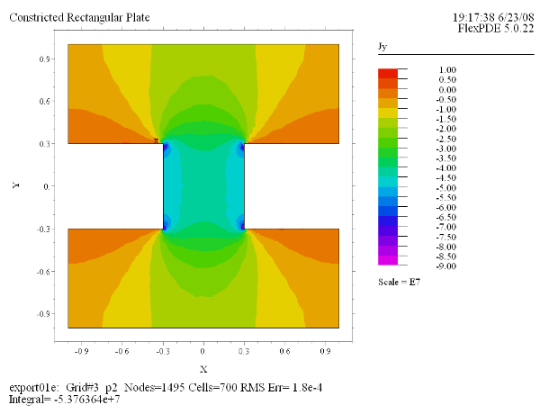
(7) Contour(Jy) painted |
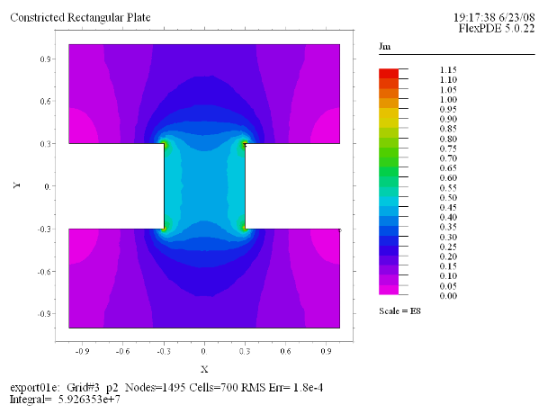
(8) Contour(Jm) painted |
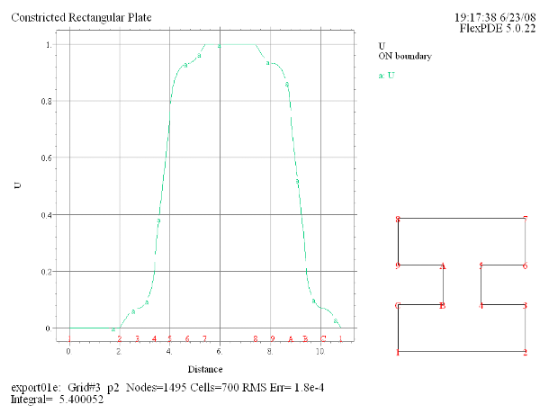
(9) Elevation(U) on 'boundary' |
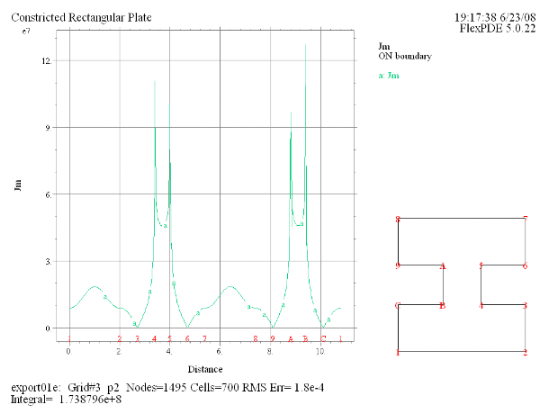
(10) Elevation(Jm) on
'boundary' |

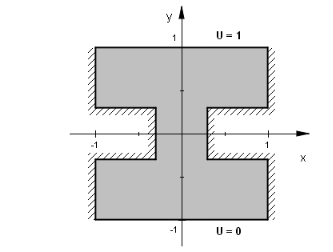 今度は右の図のようなくびれのある銅製プレート上での電導に関しFlexPDEで分析を行ってみましょう。1辺が
2 の正方形のプレートに対し、その中央部に幅が 0.6、深さが 0.7 のくびれが左右から入っているモデルを想定します。上辺に
U = 1 の電位をかけ、下辺の電位は 0 に保持、その他の境界は絶縁されているとして電流の流れを分析します。
今度は右の図のようなくびれのある銅製プレート上での電導に関しFlexPDEで分析を行ってみましょう。1辺が
2 の正方形のプレートに対し、その中央部に幅が 0.6、深さが 0.7 のくびれが左右から入っているモデルを想定します。上辺に
U = 1 の電位をかけ、下辺の電位は 0 に保持、その他の境界は絶縁されているとして電流の流れを分析します。