Sample Scripts from GB Books
GB003: 2次元における電導

4. 円形フォイル中の電導

今度は銅製の薄いフォイル中での電導の問題について考えることにします。フォイルの外周は半径 1 のチューブに、内周は同軸上にある半径 0.2 の金属棒に垂直に溶接されているものとします（共に銅製）。GB002ではz軸方向に十分な長さのある金属棒/箱の切断面において電場を考えましたが、電導性のフォイルや板の場合にはそのような前提は必要ありません。絶縁境界によって電流は x-y 平面に平行に流れることになるからです。
フォイルの内周は電位 1 に、外周は電位 0 に保たれているケースをここでは想定し、FlexPDEによる計算を実行します。

4.1 Problem descriptor [ econduction01d.pde ]

台形プレートのときの econduction01b.pde をベースにスクリプトを用意します。
TITLE
    'Radial Conduction in a Foil'    { econduction01d.pde }

SELECT
    Errlim = 3e-5

VARIABLES
    U                     { Electric potential }

DEFINITIONS
    r1 = 0.2 r2 = 1
    cond = 5.99e7         { Conductivity of Cu }
    U1 = 1.0              { Voltage }
    Ex = -dx(U) Ey = -dy(U) E = -grad(U) Em = magnitude(E)
    Jx = cond*Ex Jy = cond*Ey J = cond*E Jm = magnitude(J)
                          { Electrical current density }

EQUATIONS
    div(J)=0              { 2nd order PDE in U }

BOUNDARIES
    Region 1
      Start(r2, 0)        { Outer }
        Value(U) = 0 Arc(Center = 0,0) Angle = 360
      Start(r1, 0)        { Exclude }
        Value(U) = U1 Arc(Center = 0,0) Angle = 360

PLOTS
    Grid(x, y)
    Contour(U)    Surface(U)
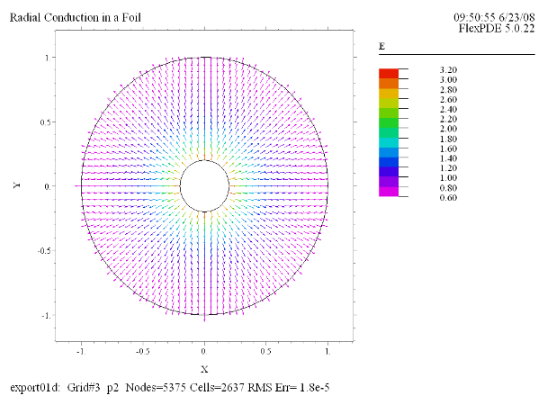
    Vector(E) norm
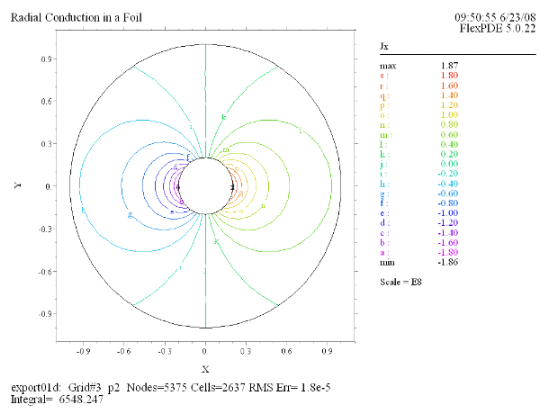
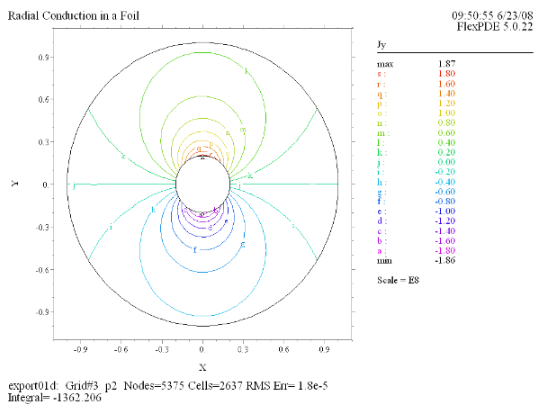
    Contour(Jx)    Contour(Jy)    Contour(Jm)

END