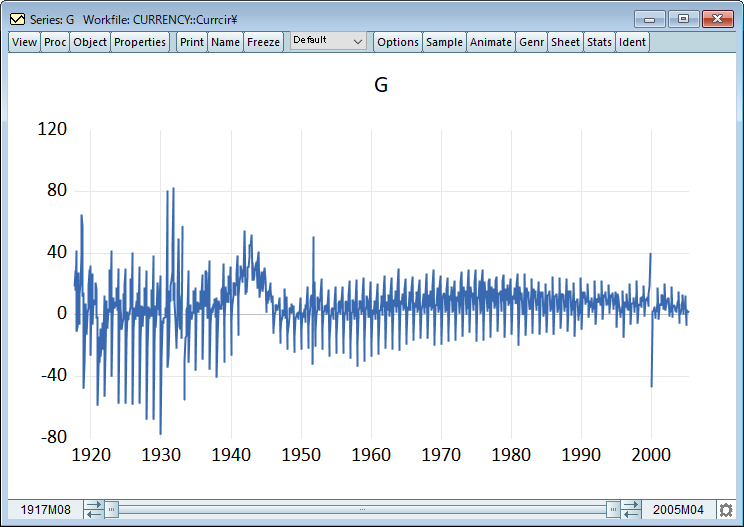
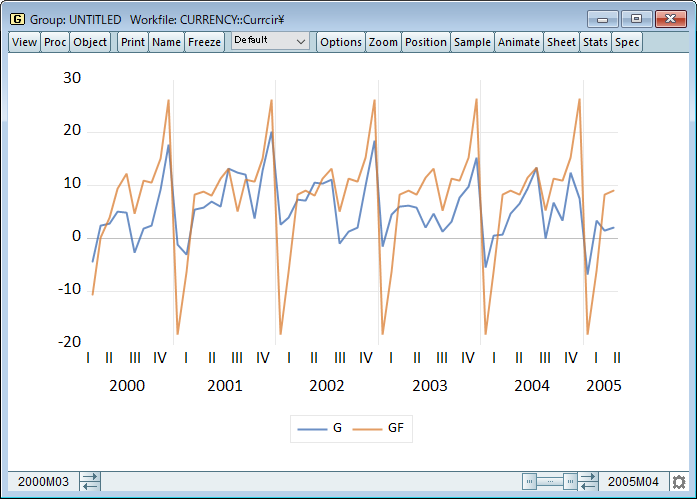
ls g @trend g(-1) @expand(@month)
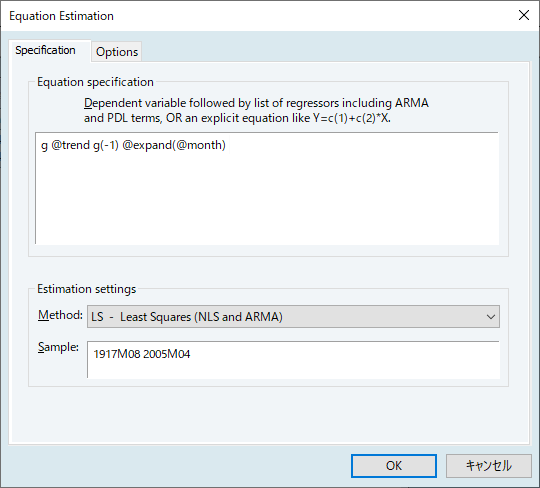
 ボタンを押してください。
ボタンを押してください。
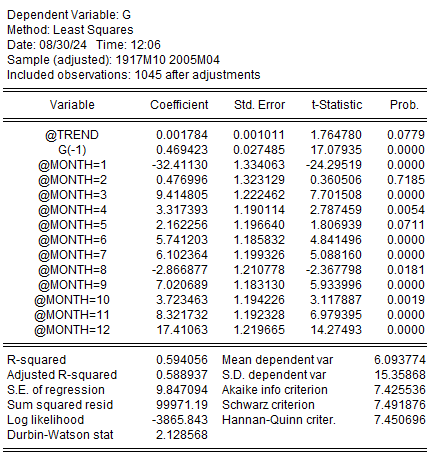
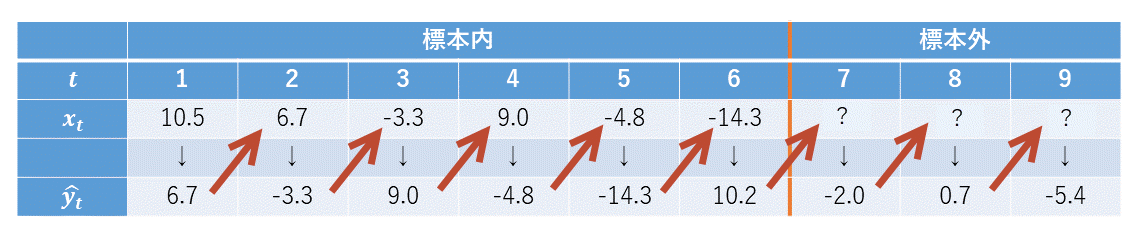
| $x$ | 推定された パラメータ |
$x$の値 | 2つの積 |
|---|---|---|---|
| トレンド項 | 0.001784 | 1047 | 1.87 |
| ラグ項 | 0.469423 | 3.4105 | 1.6 |
| 11月ダミー | 8.321732 | 1 | 8.32 |


sample wholeRange @all
sample Herodotus @first 2000
sample Heinlein 2001 @last
smpl herodotus
ls g @trend g(-1) @expand(@month)
smpl heinlein
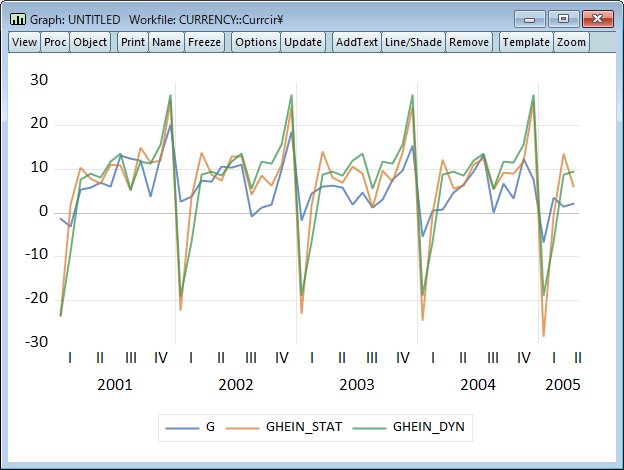
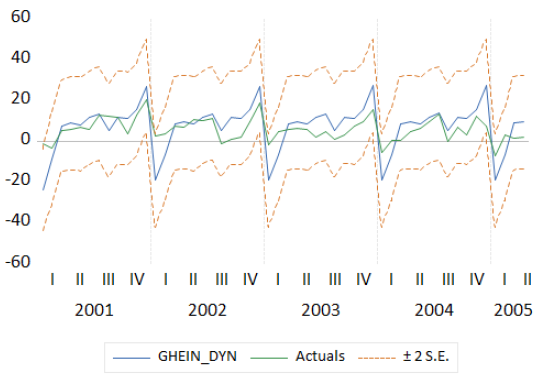
fit ghein_stat
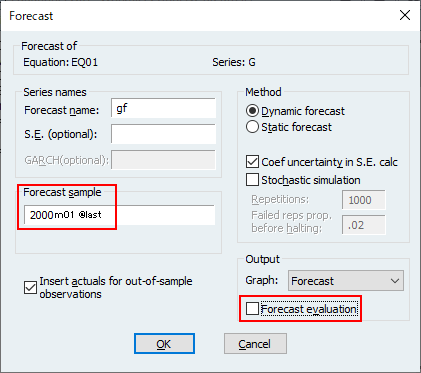
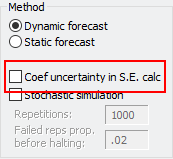
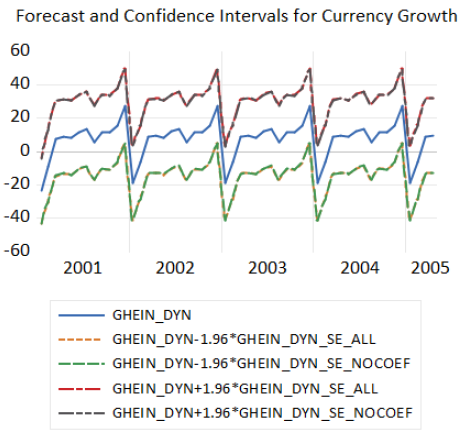
forecast ghein_dyn
plot g ghein_stat ghein_dyn

sample wholeRange @all
sample Herodotus @first 2000
sample Heinlein 2001 @last
smpl herodotus
ls g @trend g(-1) @expand(@month)
smpl heinlein
fit ghein_stat
forecast ghein_dyn
plot g ghein_stat ghein_dyn


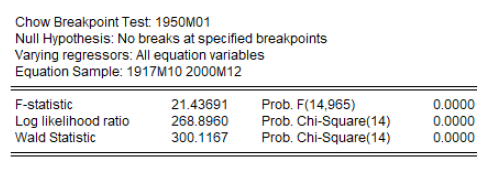
sample turtledove 1950 2000
smpl turtledove
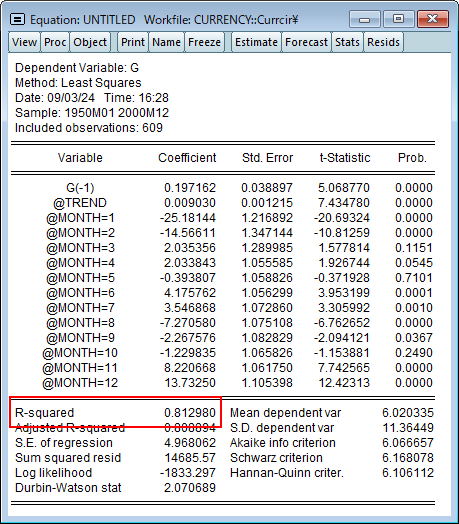

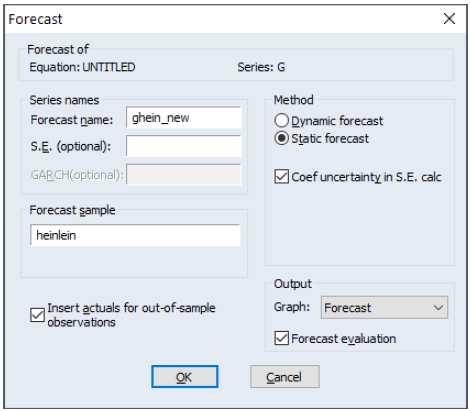
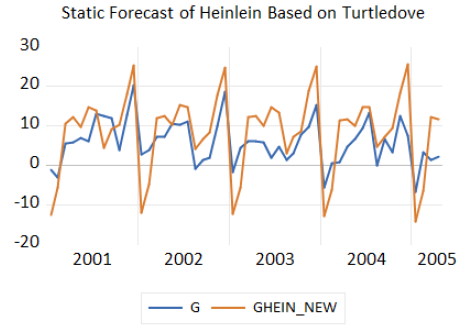
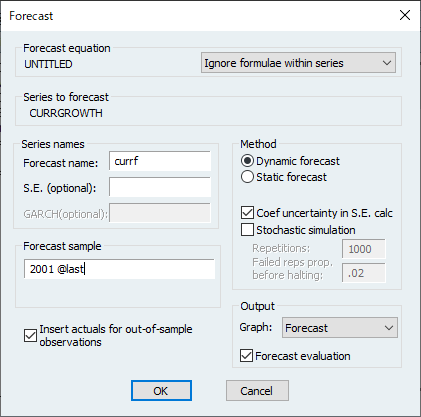
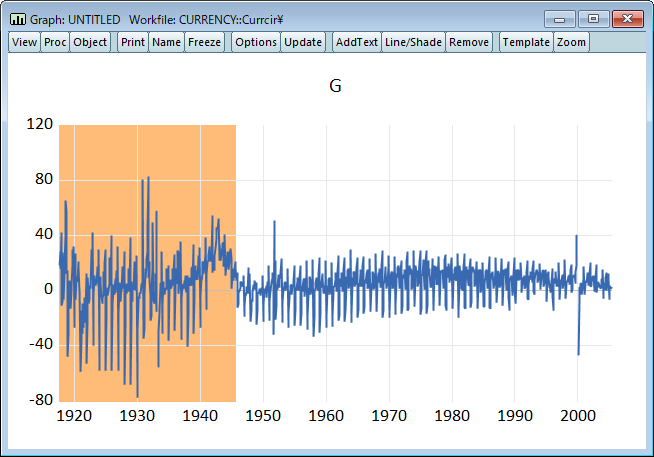
series g=1200*dlog(curr)を使用して、通貨レベルの基礎となる系列 CURR を変形したものであることがわかります。関数 dlog()は対数の 1 階差を取るものです。
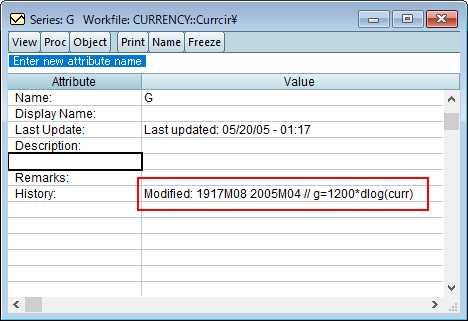
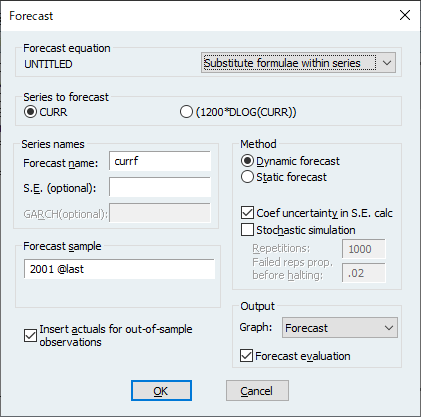
g=1200*dlog(curr)」で作成されたという情報はデータの変更履歴であり、源系列CURRとGは関連付けられていません。EViewsのautoシリーズを使用すると、EViews は CURR とautoシリーズ間の接続します。次のコマンドを使用してautoシリーズを定義し、予測式を推定できます。
smpl @all
frml currgrowth=1200*dlog(curr)
smpl @first 2000M12
ls currgrowth @trend currgrowth(-1) @expand(@month)