外れ値検出ツール

EViews 14は、シリーズ内の外れ値または推定式の残差を特定するための新しく、使いやすいツールを提供します

背景
EViewsで行う外れ値検出
実行例
影響統計量
参考文献

背景

外れ値は、他の観測値の大部分と大きく異なる値を持つ観測値です。測定エラー、データ入力ミス、またはデータの自然な変動が原因であるかに関係なく、異常値を示す観測値です。外れ値の存在は、統計分析に多大な影響を与える可能性があります。外れ値は、適切に識別および処理されないと統計結果を歪め、不正確な結論を導く可能性があるためです。
EViews 外れ値検出ビューには、系列内の外れ値を識別するためのさまざまな方法：Tukey フェンス、平均/標準偏差フェンス、ARMA 外れ値、ウェーブレット外れ値の結果が表示されます。
この機能はパネルデータでは利用できません。
Tukeyフェンス: TukeyフェンスまたはTukeyの範囲検定とも呼ばれ、Tukey (1977)によって開発されました。Tukeyフェンスは、それを超えるデータ点が外れ値と見なされる四分位ベースの間隔を定義する方法を提供します。
フェンスは上限と下限を定義し、これらの境界外にある観測値は外れ値と判断されます。フェンスは、系列の四分位範囲（$IQR$）（つまり、第3四分位（$Q_{3}$）と第1四分位$Q_{1}$の差）に基づいています。 \begin{eqnarray} 下限=Q_{1} - m \times IQR \\ 上限=Q_{1} + m \times IQR \end{eqnarray}
ここで、$m$は、データポイントが外れ値と見なされる範囲を決定するユーザー定義の定数です。通常、$m$は$1.5$に設定されますが、分析の特定のニーズに応じて調整できます。$m$の値が大きいほど、極端な値に対してより寛容になり、外れ値とされる観測値が少なくなります。
四分位数はトレンドを考慮せず、サンプル全体にわたって計算されるため、Tukeyフェンスはトレンドデータに対してはうまく機能しない可能性があることに注意してください。
平均・標準偏差フェンス: 平均/標準偏差フェンスはTukeyフェンスに似ていますが、境界が四分位数に基づくのではなく、データの平均$\mu$と標準偏差$\sigma$に基づいています。
\begin{eqnarray} 下限=\mu - m \times \sigma \\ 上限=\mu + m \times \sigma \end{eqnarray}
ここでも、$m$は、前述と同じくユーザ定義の定数です。やはり、平均・標準誤差はトレンドを考慮せず、サンプル全体にわたって計算されるため、トレンドデータに対してはうまく機能しない可能性があることに注意してください。
ARMA推定外れ値: Chen and Liu (1993)は、ARMA過程で外れ値を検出する方法を提供しています。彼らは、4つの異なるタイプの外れ値の影響を考慮しています。イノベーション的外れ値(innovational outliers)、加法的外れ値(additive outliers)、レベルシフト(level shift)、および一時的変化(temporary change)です。
Matarise et al. (2012)より抜粋した、各外れ値をグラフで表すと次のようになります。

Chen and Liuの論文では、外れ値を繰り返し特定し、外れ値を考慮してARMA係数推定値を調整するアプローチについて詳しく説明しています。EViewsで使用されるARMA外れ値検出では、Chen and Liu のステージ 1 の、次の部分のみが使用されます
- 1. 元のデータを使用して予備的なARMA推定から残差を取得します。
- 2. 4種類の外れ値効果に対応する残差と標準化された検定統計量を使用して、各観測値で外れ値の検定を実行します。4つの検定統計量のいずれかの絶対値が指定された臨界値を超える場合、観測値は外れ値とみなされます。
EViewsは、Hyndman and Khandakar (2008)の自動ラグ選択ARMA推定手順を使用します。このモデルでは、定数とトレンドが外生変数として含まれています。
ウェーブレット外れ値: ウェーブレットの特に重要かつ有用な応用の1つは、外れ値検出です(Bilen and Huzurbazar, 2002)。ウェーブレット外れ値手順については、ユーザガイドIIの「ウェーブレット外れ値検出」で詳しく説明されています。
簡単に言えば、ウェーブレット解析は離散フーリエ変換を使用して観測系列を近似し、ウェーブレットベースのスペクトル推定を実行します。
ウェーブレットは、時系列データの多重解像度解析を可能にする基底関数のファミリーです。ウェーブレットは、データをそれぞれ対応する時間間隔を持つ異なる周波数成分に分解します。時間とスケールのこの二重の局在化により、周波数と時間の両方で精度を保ちながら、複数の解像度で異常を検出できます。
Bilen and Huzurbazar (2002)のように、次のアプローチを使用して外れ値の検出にウェーブレット解析を適用します。
- 1. ウェーブレット変換を実行します。時系列データをスペクトルを表すウェーブレット係数に変換します。この分解により、急速な変化と緩やかな変化の両方についての洞察が得られます。
- 2. しきい値ウェーブレット係数: 1つ以上のスケールでウェーブレット係数のしきい値(中央値または絶対偏差など)を決定します。
- 3. 異常なウェーブレット係数を検出: しきい値を超えるウェーブレット係数は、異常な動きを示すために使用されます。
- 4. 外れ値の特定: 異常なウェーブレット係数が決定されたら、逆ウェーブレット変換を使用して元の時系列データを再構築します。この手順により、元の時系列データのどの観測値が異常な係数の原因となったかを特定できます。これらの観測値は外れ値として識別されます。
EViewsは、Bilen and Huzurbazar (2002)で使用されているものとほぼ一致するウェーブレット外れ値設定を使用します。つまり、単一スケールの時間スケール、ハードしきい値設定、False Discovery Rate (FDR) 値メソッド、および平均中央絶対偏差係数分散です。

外れ値検出ダイアログ

EViewsで単一のシリーズの外れ値検出を実行するには、シリーズを開いてView/Outlier detections...をクリックします。EViews に外れ値検出ダイアログが表示されます。

コマンドで呼び出すには次を実行します。
シリーズ名.outlier
Transformationセクションでは、元の系列で外れ値検出を実行したり、系列を変換して傾向や周期を削除したりできます。デフォルトでは元の系列が使用されます(None)が、Hodrick-Prescottフィルタ(HP filter)を選択して周期系列を使用したり、系列の1階差分を使用したり(Difference)できます。
より複雑な変換やトレンド除去/サイクリング手順は、EViews 内の別の場所で元の系列に対してそれらの手順を実行し、変換結果を保存してから、結果として得られる変換された系列に対して外れ値検出を実行することによって実行できます。
Methodセクションのチェックボックスは、どの外れ値検出方法を実行するかを制御します。デフォルトでは、すべての方法が報告されます。Fencesボックスを選択すると、EViews は Tukey フェンスと平均/標準偏差フェンスの両方を使用するように指示されます。

Optionセクションには、検出ルーチンとその出力をカスタマイズするためのさまざまなオプションがあります。

Sensitivityドロップダウンボックスを使用すると、外れ値検出方法の許容レベルを設定できます。感度は、Low、Medium、High、またはCustomから選択します。対応する値は次のとおりです。

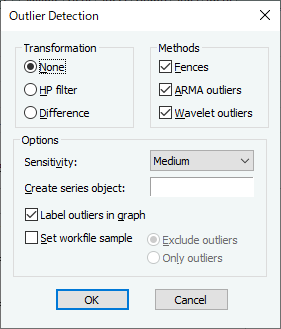
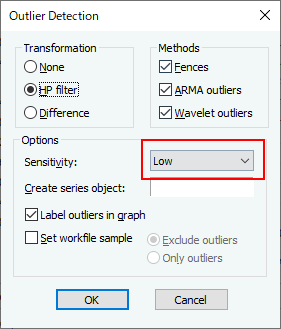
	Low	Medium	High
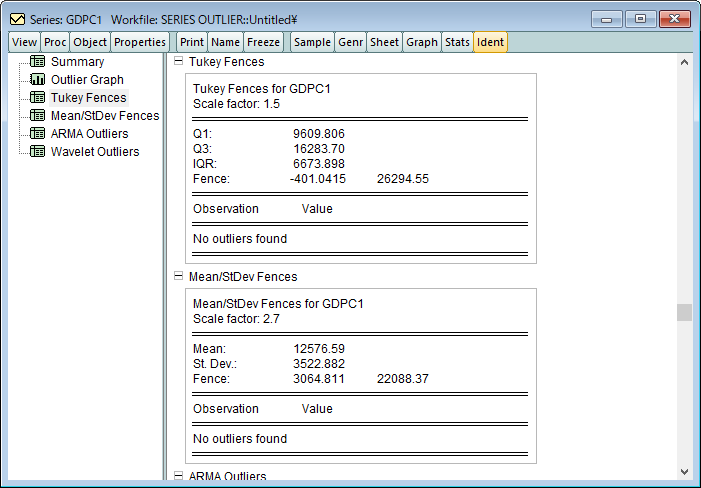
Tukey $m$	3.0	1.5	0.4
平均・標準偏差 $m$	4.7	2.7	1.5
ARMA $c$	16.0	8.0	4.0
ウェーブレット FDR	0.0005	0.001	0.01

Sensitivityは、Tukeyフェンスと平均/標準偏差フェンス、ARMA 臨界値、ウェーブレット解析の誤検出率(FDR)に対応することに注意してください。Customを選択すると、新しいダイアログが開き、これらの値を個別に設定できます。

Create series object編集フィールドに有効なオブジェクト名を入力すると、EViewsは、外れ値として識別された観測値には「1」、外れ値ではないと判断された観測値には「0」を含む新しいバイナリシリーズオブジェクトをファイルに作成します。現在のサンプル外の観測値には、NAの値が割り当てられます。
Label outliers in graphsチェックボックスをオンにすると、EViewsは出力グラフに特定された外れ値の日付ラベルを含めるようになります。
Set workfile sampleチェックボックスをオンにすると、EViewsは外れ値分析の結果を使用してワークファイルサンプルを設定します。Excluding outliersを選択すると、外れ値が除外された既存のワークファイルサンプルがサンプルに設定されます。逆に、Only outliersを選択すると、元のサンプルで外れ値として識別された観測値がサンプルに設定されます。
どちらの場合も、サンプルを設定するには作業ファイル内にシリーズが必要なので、シリーズオブジェクトの作成編集で名前を入力していない場合は、EViews によって自動的に名前が追加されます。

例題

ワークファイル「Series Outlier.wf1」には、1980年から2015年までの米国の四半期ごとの実質GDPを保持する単一のデータシリーズが含まれています。残念ながら、シリーズ GDPC1にデータ入力エラーがあり、観測値1999Q4が誤って入力されていました。
サンプルファイルは次のディレクトリにあります。
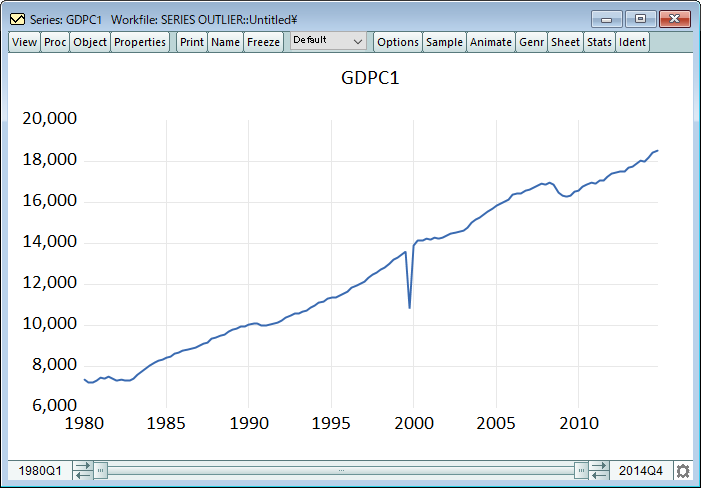
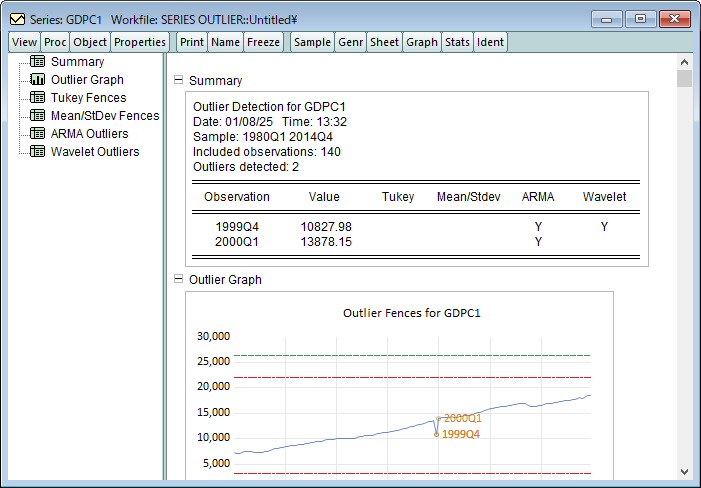
C:\Program Files\EViews 14\Example Files\EV14 Manual Data\Chapter 11 - Series\series outlier.wf1
EViewsの外れ値検出ルーチンを使用して、1999Q4が外れ値として正しく識別されるかどうかを確認できます。View/Outlier detection...をクリックし、すべてのオプションをデフォルト値のままにして、OKをクリックします。EViewsは外れ値分析を実行し、スプール出力を生成します。この出力は、個別のセクションに分割されます。
Summaryノードは外れ値検出ルーチンの概要を提供します。

要約から、2つの外れ値が検出されたことがわかります。1つは1999Q4で、もう1つはその後の期間である2000Q1です。また、Tukey法や平均/標準偏差法では外れ値は検出されませんでしたが、ARMA法とウェーブレット法の両方で1994Q4が外れ値として識別されたことがわかります。ARMA法のみが2000Q1を外れ値として識別します。
外れ値グラフノードは、元の系列、検出された外れ値、Tukeyと平均/標準偏差フェンスのグラフを提供します。

次の4つのセクションでは、個々の検出方法に関する追加情報が提供されます。Tukeyフェンスと平均/標準偏差フェンスの結果には、フェンスの構築に関連する情報が表示されます。

表には、スケール係数$m$、第 1四分位($Q_{1}$)、第3四分位($Q_{3}$)、四分位範囲($IQR$)、およびTukey外れ値の識別に使用される結果として生じるフェンス、およびスケール係数、平均、標準偏差、および平均/標準外れ値の識別に使用される対応するフェンスが示されています。どちらの方法でも、フェンスの外側に観測値がないことが報告されています。
ARMA外れ値セクションには、ARMAルーチンによって検出された外れ値と、その日付の観測値がリストされます。

Wavelet outliersセクションには、ウェーブレット法によって検出された外れ値と、平均値からの絶対偏差、および中央値からの絶対偏差がリストされます。
どちらのフェンス法も外れ値を特定していないことは注目に値します。このシリーズの元のグラフから、シリーズが強い上昇トレンドを示していることは明らかであり、これがフェンス法が外れ値を検出できなかった理由であると考えられます。この問題は、Hodrick-Prescott フィルタを使用してトレンドを取り除いた後に検出を実行することで軽減できます。View/Outlier detectionをクリックしてダイアログを表示します。
TransformセクションでHPフィルタに変更し、OKをクリックして続行します。

要約表には、外れ値の数が多く、わずかに異なるセットが表示されます。

フェンス法は両方とも外れ値を報告し、Tukey法では7つの外れ値が検出されました。特に注目すべきは、4つの方法すべてが 1999Q4 が外れ値であることに同意していることです。
グラフには、7つの外れ値と2セットのフェンスが表示されます。
Tukeyフェンスによって外れ値として検出された観測値の一部は、周期的なデータの自然な変動から生じる可能性があります。観測値が外れ値であるかどうかの基準をより厳しく設定したい場合があります。View/Outlier detectionをクリックしてダイアログを表示します。

感度をLowに変更し、OKをクリックします。結果を見ると、感度が低いと2つの外れ値が検出されます。

1999Q4は、4つの方法すべてで依然として検出されています。

影響統計量

影響統計量(influence statistics)は、影響力のある観測値、つまり外れ値を発見する方法です。これは、1つの観測値が回帰結果に及ぼす影響、つまり方程式に含まれるサンプル内の他の観測値と、どの程度異なるかを測定するものです。EViewsでは、RStudent, DRResid, DFFITS, COVRATIO, HatMatrix, DFBETASの6種類の影響統計量を利用できます。

RStudent はスチューデント化残差です。つまり、その観測値における方程式の残差を標準偏差の推定値で割ったものです。 \begin{eqnarray} \overline{e_{i}} = \frac{e_{i}}{s(i)\sqrt{1-h_{i}}} \end{eqnarray} $e_{i}$はその観測値のオリジナルの残差、$s(i)$は$i$番目の観測値がモデルに含まれなかった場合の残差分散、$h_{i}$はハット行列における$i$番目の対角要素、$x_{i}(X'X)^{-1}x_{i}$です。RStudent は、元の方程式にダミー変数（特定の観測値では $1$、その他の観測値では$0$）を代入した場合に得られる$t$統計量と数値的に同一です。したがって、これはその観測値の有意性の検定として解釈できます。
DFFITSは、元の式とその観測値なしで推定された式との間の、その観測値の適合値のスケーリングした差です。スケーリングは、差を適合の標準偏差の推定値で割ることによって行われます。 \begin{eqnarray} DFFITS_{i} = \bigg[\frac{h_{i}}{1-h_{i}} \bigg]^{1/2}\frac{e_{i}}{s(i)\sqrt{1-h_{i}}} \end{eqnarray}
DRResidはドロップされた残差を示します、その観測データなしで方程式を推定した場合のその観測の残差の推定値です。
COVRATIOは、元の方程式の係数の共分散行列の行列と、その観測値を除いた方程式の共分散行列の行列式の比です。
HatMatrixはハット行列における$i$番目の対角要素$x_{i}(X'X)^{-1}x_{i}$です。
DFBETASは、元の方程式と、それぞれの観測値を含まず推定された方程式の間の、推定された係数の差を、係数の分散でスケーリングしたものです。 \begin{eqnarray} DFBETAS_{i,j}=\frac{\beta_{j}-\beta_{j}(i)}{s(i)\sqrt{\rm{var}(\beta_{j}})} \end{eqnarray}

影響統計量を求める場合はView/Stability Diagnostics/Influence Statisticsと操作します。

EViewsは求める統計量とその表示方法を決めるダイアログを表示します。統計量はOutput statisticsボックスで選択し、その値をseriesに保存する場合はその名前を隣のボックスに入力します。チェックボックスをチェックしますが、名前の項目はオプションです。DFBETAS統計量のボックスに入力する情報はseries名ではなく, 新たに作成されるseriesのサフィックスです。EViewsは推定式の係数ごとにseries名の後ろにサフィックスを付けたシリーズを新たに作成し、計算結果を保存します。
Output typeの項目では、求めた影響統計量の表示方法をグラフと表から選択します。両方ともチェックするとEViewsはグラフと表を画面に表示します。

表形式の出力を選択すると、ダイアログの右側に表の様式を設定するオプションを表示します。デフォルトでは統計量を100行分しか表示しません。デフォルトの状態ではDisplay in observation orderにチェックが付いていますので、データの順番にしたがって表示します。
rdchem.WF1ワークファイルの方程式E1を使用して説明します。サンプルファイルは下記のフォルダに格納されています。
C:\Program Files\EViews 14\Example Files\EV14 Manual Data\Chapter 26 - Specification and Diagnostic Tests
モデルオブジェクトE1を開いて、View/Stability diagnostics/Influence statisticsと操作します. そのままOKをクリックして計算を行います.
DFFITSとCOVRATIOのプロットを見ると、10番目の観測値が外れ値であることがはっきりとわかります。

表形式の出力では、外れ値に該当する部分は赤字で示されます。

参考文献

Bilen, C., and Huzurbazar, S. (2002). Wavelet-Based Detection of Outliers in Time Series. Journal of Computational and Graphical Statistics, 11(2), 311–327. https://doi.org/10.1198/106186002760180536
Chen, Chung, and Lon-Mu Liu. “Joint Estimation of Model Parameters and Outlier Effects in Time Series.” Journal of the American Statistical Association, vol. 88, no. 421, 1993, pp. 284-97.
Hyndman, R, and Khandakar, Y. (2008), “Automatic Time-Series Forecasting” Journal of Statistical Software, 27, 1–22.
Matarise, Florance, Lawrence Dhliwayo, Immaculate Susan Nduna, Innocent Maposa, Lillian Siziba. (2012). "Detecting Level Shifts, Temporary Changes and Innovational Outliers in Intervention Analysis" International Journal of Statistics and Systems, vol.7, no. 3, pp. 241–254.
Tukey, John W (1977). Exploratory Data Analysis. Addison-Wesley. ISBN 978-0-201-07616-5. OCLC 3058187.