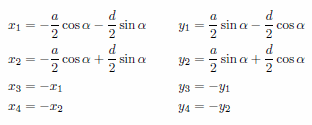Sample Scripts from GB Books
GB011: 2次元の完全流体
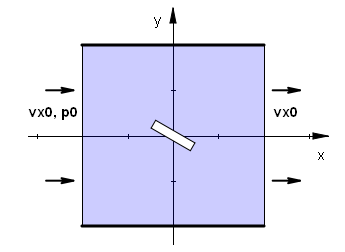
4. 傾斜した平板のまわりの流れ
|
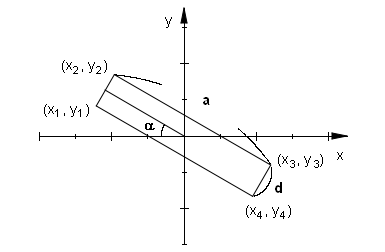
今度は流れの中に平板を斜めに配置したときに、平板にかかる力について分析してみます。流れについてはこれまでと同一の条件、すなわち入口での流速 vx0、圧力 p0、出口での流速 vx0 を仮定します。板の流れに対する角度を α 、板の幅と厚みをそれぞれ a = 0.5, d = 0.1 としたとき、板の4隅の座標値は次のように与えられる点に注意してください。なお、ここでは α = PI/6 のケースについて計算を行います。
|
4.1 Problem descriptor [ pfluid01d.pde ]
|
まずタイトルを設定します。 従属変数を定義します。ポテンシャル流れの場合には一つのスカラー変数(速度ポテンシャル)のみによって流れがすべて規定されます。 関連するパラメータや数式を定義します。最後のbrute_forceという式にかかっている
2*y2 という式は
y2 - y4
を意味し、板の流れの方向(x方向)への射影面積(z方向には1を取る)に対応します。 ポテンシャル流れを規定するラプラス方程式を記述します。 BOUNDARIESセクションにおける設定のしかたはこれまでのケースと
同様です。 最後に出力すべき情報を規定します。 |
4.2 実行結果
|
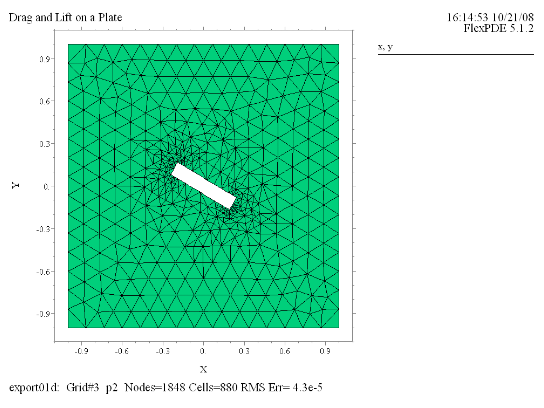
(1)
Grid(x, y) |
|
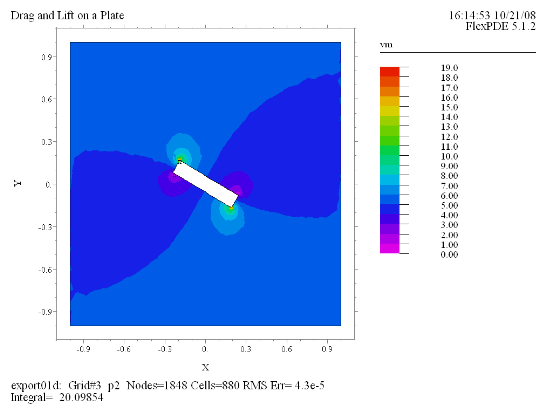
(2)
Contour(vm) painted |
|
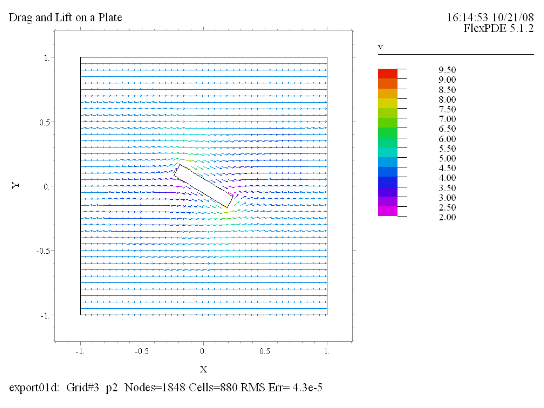
(3)
Vector(v) norm |
|
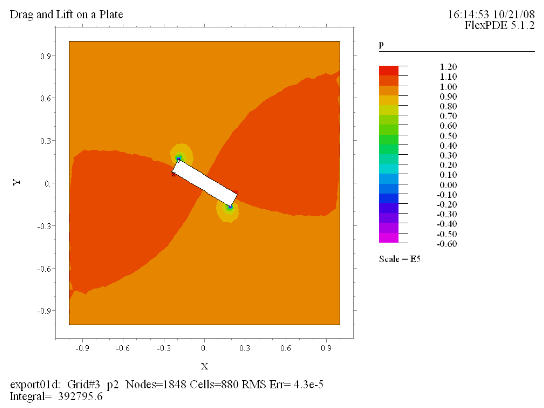
(4)
Contour(p) painted |
|
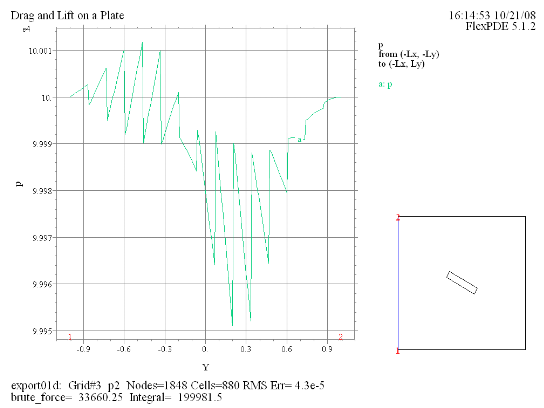
(5)
Elevation(p) from
(-Lx, -Ly) to (-Lx, Ly) Report(brute_force) |
|
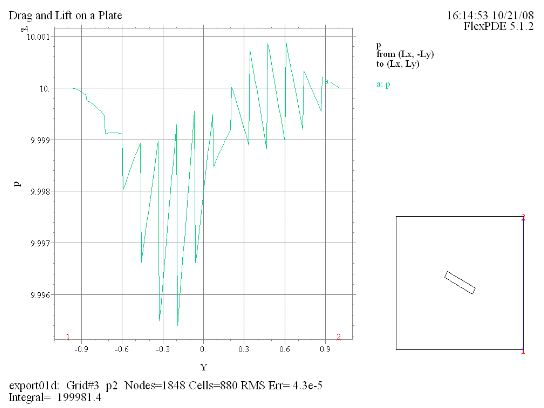
(6)
Elevation(p) from
(Lx, -Ly) to (Lx, Ly) |
|
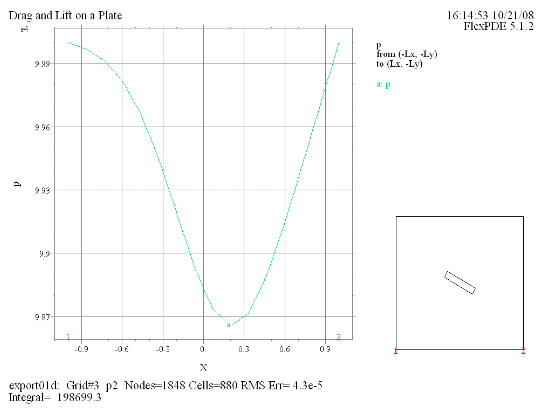
(7)
Elevation(p) from
(-Lx, -Ly) to (Lx, -Ly) |
|
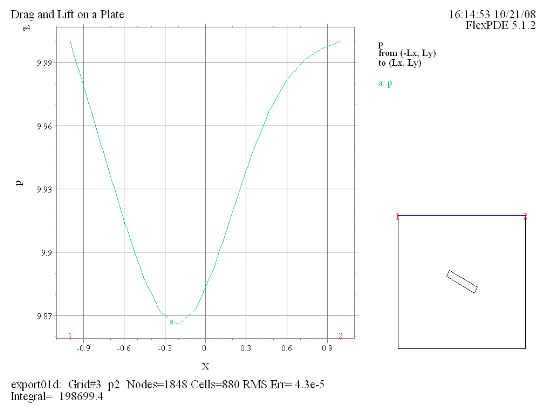
(8)
Elevation(p) from
(-Lx, Ly) to (Lx, Ly) |
|
プロット(5)-(8)の線積分値の結果が示唆するところは、平板に対してdragやliftというnet forceが全く働いていないということです。実際ポテンシャルフローの場合にはこのような結果になることが解析的に示されています。これは常識と矛盾する結果であるわけですが、その原因は粘性を全く持たない完全流体を仮定したことに起因しています。より現実に即した結果を導くためには粘性に配慮したモデルを考える必要があります。 |