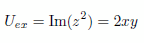Sample Scripts from GB Books
ラプラス方程式、ポアッソン方程式
今度は解析対象のドメインを四分円としてラプラス方程式を解いてみます。検証用の厳密解としては |
|
(4) |
を想定し、境界条件はすべてDirichlet型で設定することにします。 |
1. Problem descriptor [ laplace01e.pde ]
最初に作成したスクリプト laplace01a.pde に対し修正を施したものを示しておきます。円弧の境界を設定するにはArc文を使用します。 |
2. 実行結果
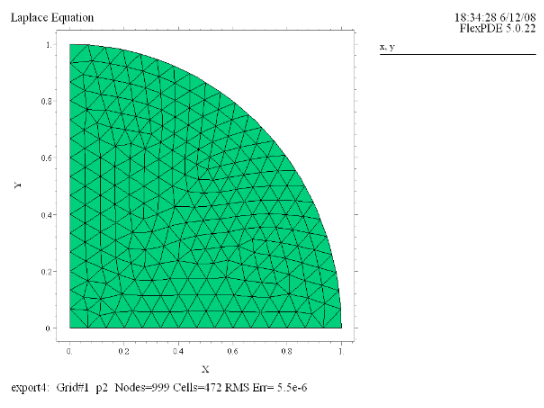
(1) Grid(x, y) |
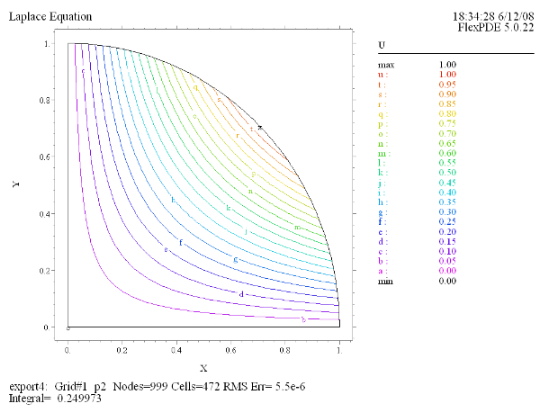
(2) Contour(U) |
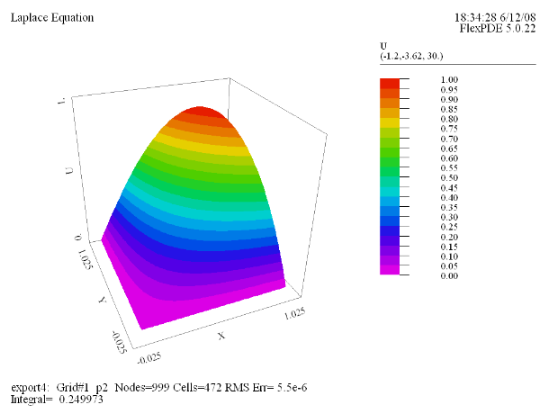
(3) Surface(U) |
(4) Contour(U_ex) |
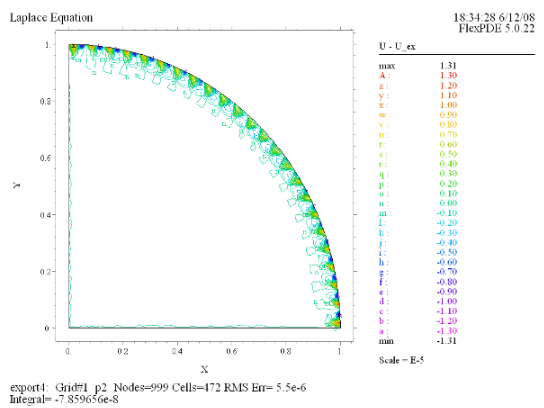
(5) Contour(U - U_ex) |