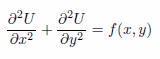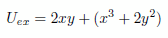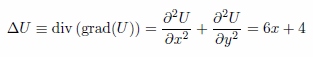Sample Scripts from GB Books
ラプラス方程式、ポアッソン方程式
ポアッソン方程式はラプラス方程式に似てはいますが、右辺が0ではなく関数となる点が異なります。 |
|
(5) |
ポアッソン方程式の厳密解を求めることは一般的に困難ですが、解を想定した上でそれに対応したPDEを導くことは簡単に行えます。例えば |
|
(6) |
という解を想定した場合、第1項の 2*x*y は調和関数(ラプラス方程式を満たす関数)ですから、ラプラシアンは0となります。従って数式(5)の f(x, y) に寄与するのは第2項の (x^3 + 2*y^2) の部分のみということになります。従って解(6)が満足するポアッソン方程式は次のようになります。 |
|
(7) |
このPDEをFlexPDEで解いた結果がどの程度厳密解(6)に一致するかを検証してみます。解析対象のドメインは正方形領域とし、境界上では関数(6)の値をValue文で与えるものとします。 |
1. Problem descriptor [ laplace01f.pde ]
TITLE |
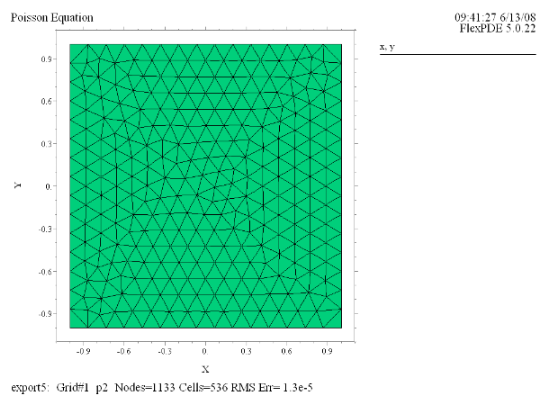
2. 実行結果
(1) Grid(x, y) |
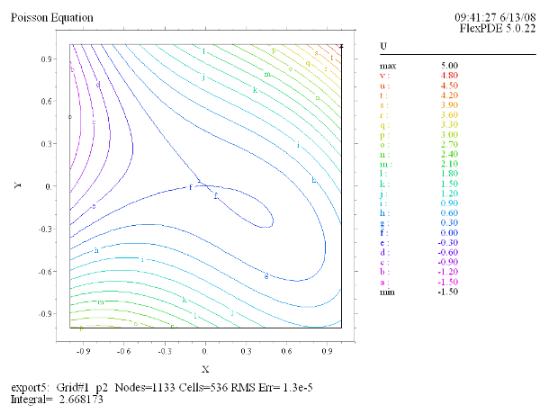
(2) Contour(U) |
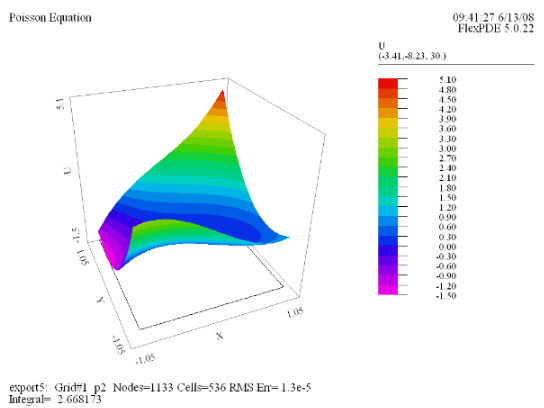
(3) Surface(U) |
(4) Contour(U_ex) |
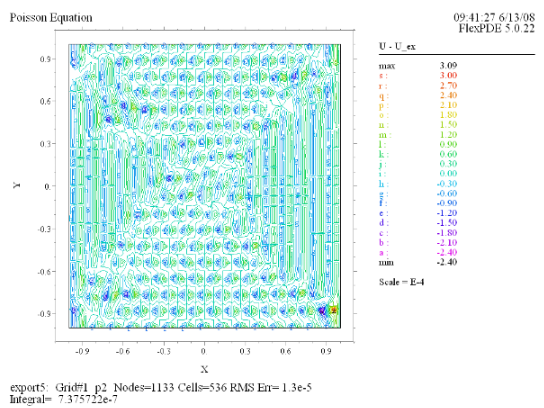
(5) Contour(U - U_ex) |