Sample Scripts from GB Books
GB005: 1次元/2次元過渡問題
4. 鉄棒からの2次元熱拡散
以下に示すスクリプトの中では従属変数 temp に対し threshold = 0.1 という指定が行われている点に注意してください。これより小さな温度変動に対しては興味がないことを示すもので、計算時間の短縮に効果があります。 |
4.1 Problem descriptor [ transient01d.pde ]
基本形は transient01a.pde と変わりません。 |
4.2 実行結果
ここでは出力結果の一部のみを紹介するに留めます。 |
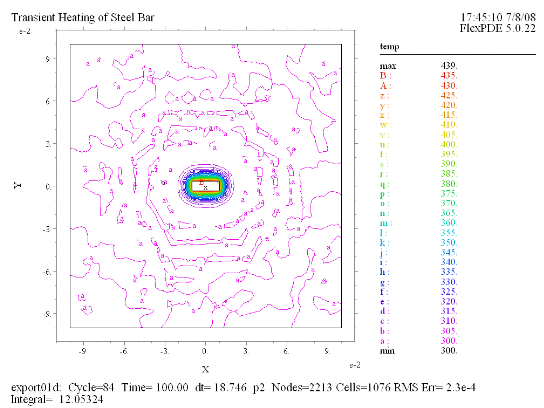
(1) Contour(temp) at t =
100 |
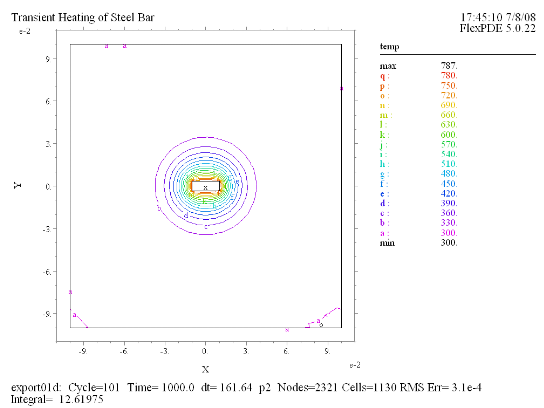
(2) Contour(temp) at t =
1000 |
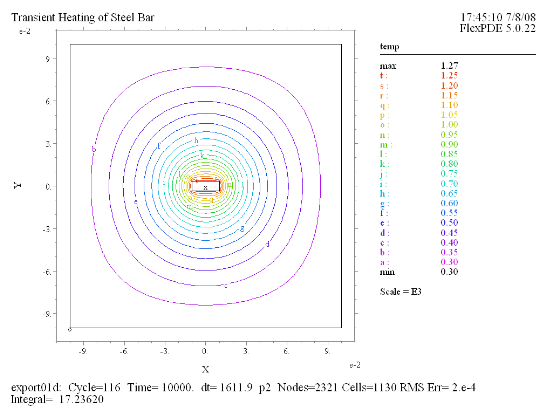
(3) Contour(temp) at t =
10000 |
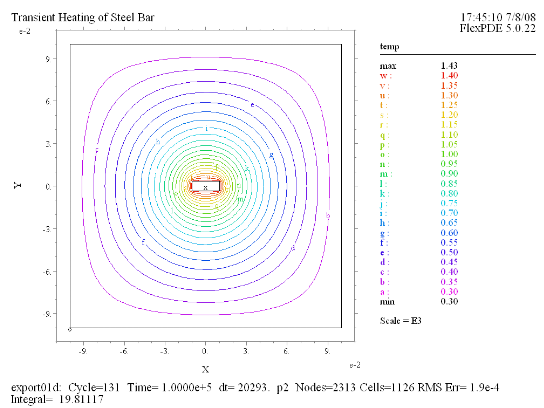
(4) Contour(temp) at t =
1e5 |
(5) Contour(temp) at t =
1e6 |
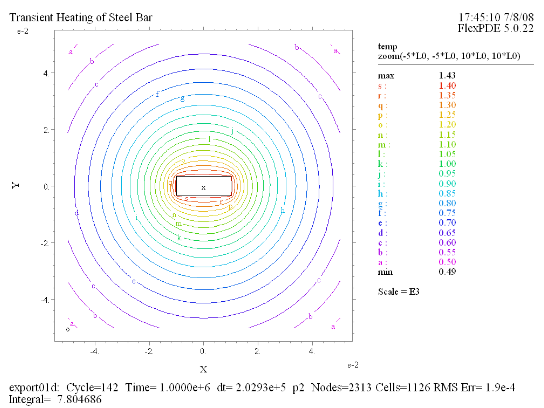
(6) Contour(temp)
zoom(-5*L0, -5*L0, 10*L0, 10*L0) at t = 1e6 |
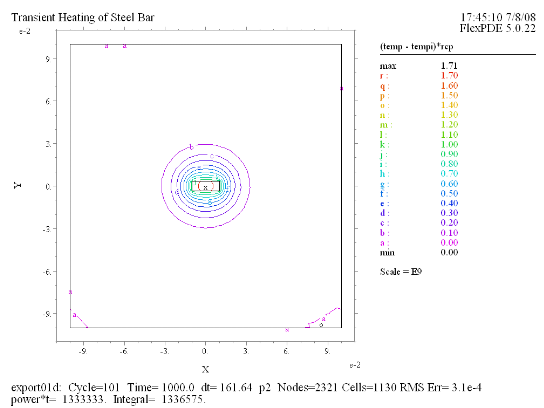
(7) Contour((temp -
tempi)*rcp) Report(power*t) at t = 1000 |
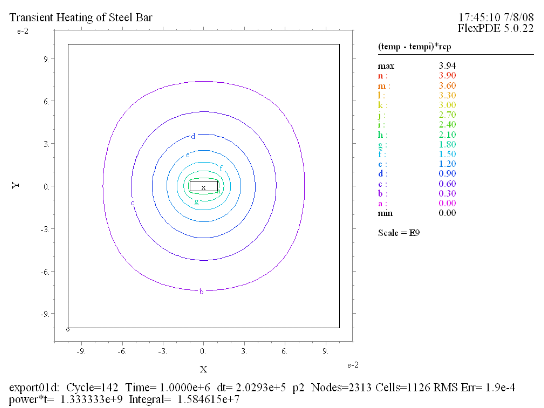
(8) Contour((temp -
tempi)*rcp) Report(power*t) at t = 1e6 |

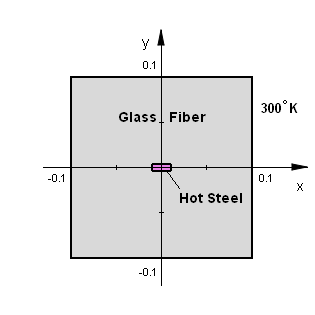 ここまでは本質的に1次元の問題を便宜的に2次元のモデルとして扱ってきたわけですが、今回は2次元における熱伝導の問題を正面から扱うことにします。右図中央にあるのは断面が長方形の鉄製の棒で、電磁誘導によって熱せられるものとします。周囲は熱伝導率の低いガラス繊維によって囲まれており、その外側を囲う正方形の箱は一定温度300度Kに保たれているものと仮定します。
ここまでは本質的に1次元の問題を便宜的に2次元のモデルとして扱ってきたわけですが、今回は2次元における熱伝導の問題を正面から扱うことにします。右図中央にあるのは断面が長方形の鉄製の棒で、電磁誘導によって熱せられるものとします。周囲は熱伝導率の低いガラス繊維によって囲まれており、その外側を囲う正方形の箱は一定温度300度Kに保たれているものと仮定します。