Sample Scripts from GB Books
GB004:  2次元熱伝導

前の例では外界との境界条件としてDirichlet型を想定して計算を行いましたが、今度はNeumann型の境界条件を設定してみます。すなわち0度Cの水を強制対流（forced convection）させることで冷却を行うものとします。その場合、境界上では

という条件を適用することになります（ニュートンの冷却の法則）。今、比例定数を50とするとFlexPDEに対してはValue文の代りに
Natural(temp) = 50*(temp - 273)
という文を指定すれば良いことになります。

ここでは hconduction01b.pde に対する変分のみを記すことにします。
  TITLE
    'Heated Semi-Circular Rod, Convection'    { hconduction01c.pde }
  ...

境界条件をValue文からNatural文に変更します。
  BOUNDARIES
    Region 1  k = 3.5  heat = 0             { Granite, default }
      Start 'outer' (-Lx, -Ly)  Natural(temp) = 50*(temp - 273)
        Line to (Lx, -Ly) to (Lx, Ly) to (-Lx, Ly) to Close
    （Region 'steel'の定義はそのまま残す）

PLOTSセクションにおいては外周上における温度の値をプロットするためのElevation文を追加します。
  PLOTS
    ...
    Elevation(temp) on 'outer'
    ...

  END

(1) Grid(x, y)
ほとんど前のケースと変わりませんが、セルの数は若干少なくて済んでいます。

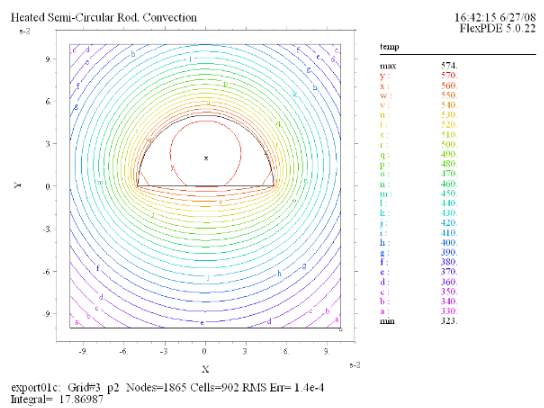
(2) Contour(temp)
ドメイン全体としての等温線図は次のようになります。 前のケースと比べると全体的に温度が高くなっている点に注意してください。特に最高温度は100度以上高くなっています。

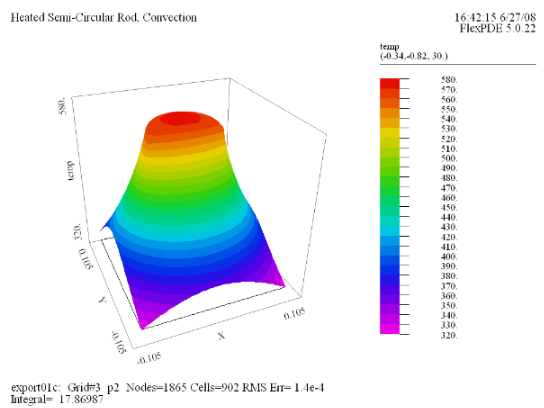
(3) Surface(temp)
温度 T(x, y) の曲面の形状をプロットしたものです。 外周上の温度は273度よりかなり高くなっています。

(4) Contour(temp) painted on 'steel'
鋼材部分のみのより詳しい等温線図です。

(5) Vector(fluxd) norm
熱流束密度 f のベクトルプロットを示したものです。

(6) Contour(fluxd_m) painted
熱流束密度ベクトル f の絶対値に関する等高線図です。

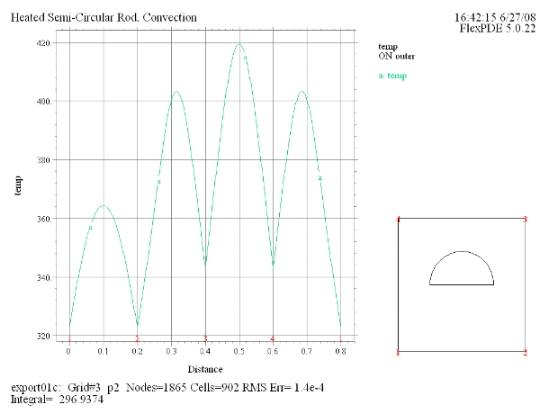
(7) Elevation(temp) on 'outer'
外周上における温度の値をプロットしたものです。前の例では273度一定に保たれていたわけですが、今回の場合には周囲の冷却水の温度より150度近くも高くなっている部分があることがわかります 。

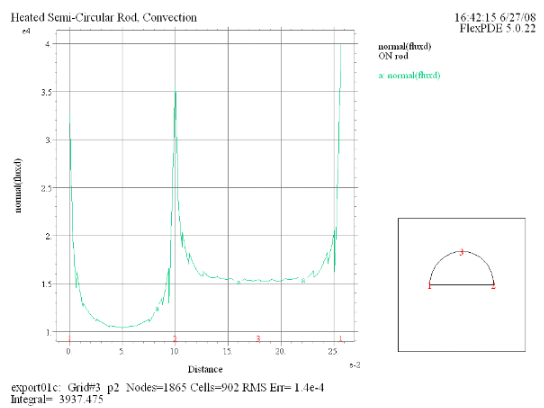
(8) Elevation(normal(fluxd)) on 'rod'
鋼材外周上での熱流束密度ベクトル f の外向き法線成分の値をプロットしたものです。 境界上での積分値は 3937 という値になっています。

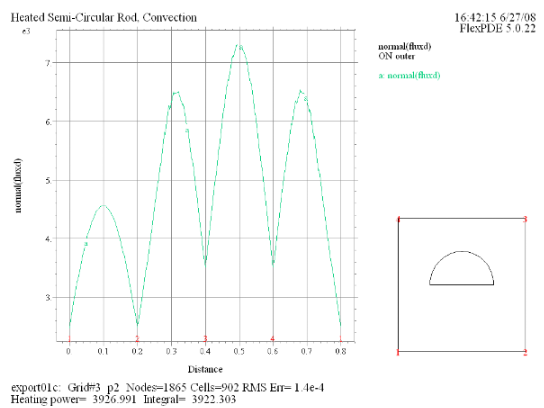
(9) Elevation(normal(fluxd)) on 'outer' Report(PI*r0^2/2*1e6) as 'Heating power'
外部境界上での熱流束密度ベクトル f の外向き法線成分の値をプロットしたものです。境界上での積分値は 3922 という値になっています。理論値 3927 は前の例の場合と同一です。