従来手法では難しい課題をベイズ推論で解決
測定したスペクトルデータから複数のピークを見つけ、ピークの数や位置、広がり、面積など、ピークの特性値を求めることは、さまざまな研究分野で重要な解析課題です。
このようなピーク分析は、OriginProなどの解析ソフトウェアを使い、ピーク検出や非線形曲線フィット(Levenberg-Marquardtアルゴリズムなど)の機能を利用することで、多くのケースに対応することができます。ところが、データが粗かったり、ノイズが乗っているような場合、解析することが難しくなります。
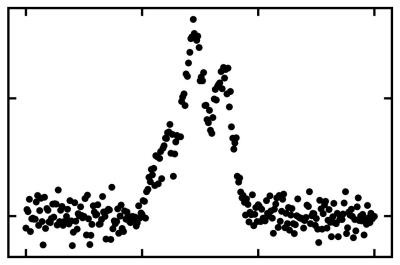
例えば、下図のようなスペクトルデータを解析するケースではどうでしょうか。まず、ピークがどこに何個あるか求めるところから困難に直面します。
従来手法のピーク検出アルゴリズムには、部分的な最大・最小値を数える、一次微分する、二次微分する、一次微分後の残差を利用するなど、さまざまなアプローチがありますが、どの手法もノイズの上下動を拾ってしまい、実際は検出したくない数多くのピークを検出します。
対処方法としては、不要なピークを検出しないためにフィルタリングを行う、事前にスムージングを行う、自動検出をあきらめて解析者がピークの個数を指定するといった対応を行う必要があるでしょう。
しかし、できるだけ解析者の恣意的な判断を排除したい場合や、そもそも解析者自身が何個のピークがあるのか判断に迷う場合、どうしたらよいでしょうか。
ノイズの大きなデータを解析しなければならない、という課題がある
この図のような粗いデータを解析したいというケースは珍しくありません。
例えば、スペクトルを得るために試料にX線を照射する測定では、解析対象の試料にX線を長時間照射することで、試料を破壊してしまうことがあります。当然、長時間測定することができず、低ノイズのデータを得ることができません。
試料の特性上、低ノイズのデータを得られないケース
| X線を長時間照射 | → | 試料が破壊されてしまう |
| X線を短時間照射 | → | 測定データのS/Nが悪い(分析が難しい) |
一方で、測定時間を短縮したいという課題を抱えている場合もあります。大量の試料を解析しなければならないようなケースです。
長時間測定すれば低ノイズのデータを得ることができ、解析しやすくなります。試料が破壊されることもなく、長時間測定が物理的に可能だとしても、1000個の試料を解析しなければならないとしたらどうでしょう。
1つの試料の測定に数時間もかけているわけにはいきません。短時間の測定で得られるS/Nが悪いデータを解析可能だとすれば、とても助かります。
大量の試料を測定するケースでは個々の測定を短縮したい
| 長時間測定の課題 | → | 大量データの測定に膨大な時間 |
| 短時間測定の課題 | → | 測定データのS/Nが悪い(分析が難しい) |
このような課題を解決する1つの方法として、当社はベイズ推論を利用したピーク分析を行いました。
1. 実際にベイズ推論で解析!
データが観測される過程はノイズを伴った確率モデルとして記述することが出来ます。ベイズ推論は、データの生成モデルと推定対象の事前情報を事前確率として用いて、得られたデータのもとで生成モデルに含まれる情報を確率分布として計算する統計的手法です。
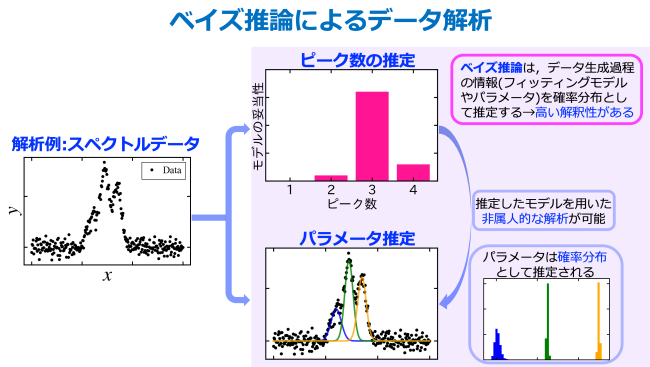
この事例では、図のようなスペクトルデータに対してベイズ推論を用いてピーク分析を行いました。最終的に求めたい結果は、ピークの個数と位置です。
ピーク数の推定
生成モデルには観測ノイズ、データ生成のモデル、モデルパラメータなどに関するさまざまな情報が含まれ、これらはベイズ推論によって推定することが出来ます。このとき、推定結果は確率分布として得られるので、その統計量を計算することで定量的に結果の信頼度を評価することができます。
ベイズ推論によりピーク数を推定したところ、下図に示すようにピーク数は3個の可能性がいちばん高いという結果が得られました。このように、推定結果が1つの値として得られるのではなく、確率分布として得られることがこの推定手法の特徴です。
パラメータの推定
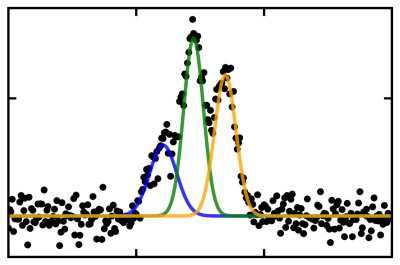
ピーク数を3個と決定し、ピークフィッティングを行いました。
ピークのモデルにはGauss関数を仮定し、解析を行いました。ピーク位置についても結果が確率分布で得られることが従来手法と異なる点で、結果の信頼度を定量的に評価できます。いちばん確率が高い位置を結果として採用し、下図のように各ピークの位置を求めることができました。