従来手法では難しい課題をベイズ推論で解決
近年、ベイズ推論によりデータ解析を行う手法が注目されています。
ベイズ推論は、データの生成過程を確率的にモデリングし、得られたデータのもとで生成モデルに含まれる情報を確率分布として計算する統計的手法です。ベイズ推論によるデータ解析アルゴリズムは、高い精度と解釈性を備えています。
迷惑メールのフィルタリングに利用されているとか、機械学習との相性がよいといった話はよく耳にする機会がありますが、スペクトル解析などの科学技術分野でも活用される例が目立ってきました。
特に、従来手法では解くことが難しい問題に対処する新しいツールとして、ベイズ推論によるデータ解析は強い力を発揮します。
では、いったいベイズ推論を使うことで何ができ、強みはどのようなことなのでしょうか。
1. ベイズ推論の強み
ベイズ推論を使って解析を行うことの強みはさまざまありますが、特に大きなメリットとなるものは、以下の3つです。
S/Nの悪いデータや欠損データの解析ができる
最小二乗法などのアルゴリズムでは解析することが困難な、大きなノイズを伴ったデータや欠損のあるデータに対して、ベイズ推論を用いた解析が有効です。
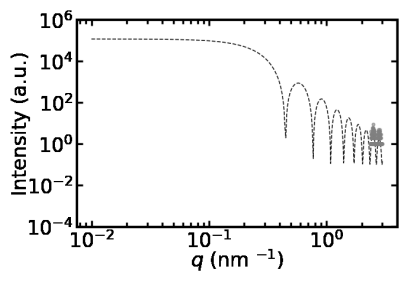
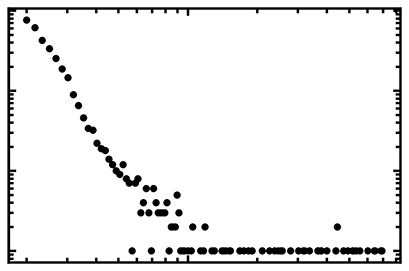
以下のグラフをご覧ください。このようにS/Nが悪いデータや欠損があるデータがあります。果たして解析できるでしょうか。特に、2つ目のデータではグラフの右端のほんのわずかな部分しか測定データがありません。
最小二乗法などの従来手法のアルゴリズムでは、このように大きなノイズを伴ったデータや欠損のあるデータに対して対処することは困難です。こうした場合、ベイズ推論を用いた解析が有効です。
こちらがベイズ推論を使い、実際に解析した結果です。本当にこのような結果が出るの? と驚かれた方もいらっしゃるのではないでしょうか。
これまで解析をあきらめていたデータも、ベイズ推論を使うことで解析できるかもしれません。
解析結果の信頼度の評価、数理モデルの定量的な比較・選択が可能
ベイズ推論を用いると、データ解析で得られた結果の信頼度を定量的に評価することができ、モデルの妥当性を定量的、理論的に評価・選択することも可能です。
信頼度が低い結果が得られた場合、解析手法の変更やデータの取り直しといった意思決定の手助けにもなります。
2. 補足資料
ベイズ推論が得意とする解析
これらの解析は、ベイズ推論が特に得意としています。
従来手法で解析できず困っているデータがあれば、ベイズ推論を利用することもぜひご検討ください。
- フィッティングモデルの定量評価・選択
- モデルのパラメータ推定
- 解析結果の信頼度評価
さまざまなデータに対して適用可能
ベイズ推論は物性実験データを始め、さまざまな分野のデータに対して有効な手法です。
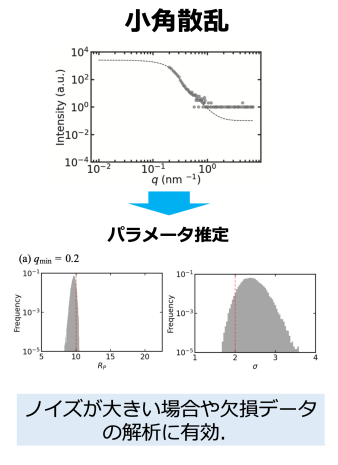
例えば、反射スペクトル、メスバウアー、X線・中性子線小角散乱のデータに対して適用できます。
解析事例能
こちらの2つの事例は、実際にベイズ推論を用いて解析を行った事例です。小角散乱とメスバウアースペクトルの解析事例です。