ISO27001(ISMS)認証
情報セキュリティ・マネジメントシステム
© 2025 Lightstone Corp. All Rights Reserved
【ウェビナーのお知らせ】
「Stataで学ぶ共分散構造分析／構造方程式モデリングウェビナー」を開催します。
下記リンクより概要をご覧ください。
はじめに
構造方程式モデリング（SEM, Structural Equation Modeling）とは、仮説に基づいて変数間の関係をモデル化し、 そのモデルをデータに当てはめて検証する分析手法です。共分散構造分析とも呼ばれます。 心理学や計量経済学などの分野で利用され、アンケート結果のデータなどから、定量的に計測できない変数間の関係性をモデル化することができます。
構造方程式モデリングでは、観測可能な変数（観測変数）と観測されない潜在的な変数（潜在変数）の因果関係を仮説に基づいてモデル化します。 潜在変数間の関係を表現することができ、仮説の妥当性を検証する際に有用な分析手法です。
以下では、構造方程式モデリングの概要についてご紹介します。
1. SEMで表現できる統計モデル
さまざまな種類の統計モデルを表現するための非常に柔軟な手法です。
SEMを使用することで、観測データや潜在変数間の複雑な関係をモデル化し、因果関係や相関を解析することができます。
以下は、SEMを用いて表現できる代表的な統計モデルの一例です。
- パス解析
- 複数の変数間の因果関係を図式化し、統計的に検証する手法です。回帰分析を拡張し、直接的・間接的な影響を明確にし、因果モデルの妥当性を確認します。
- 媒介分析
- ある変数が他の変数間の関係にどのように影響を与えるかを調べる手法です。 独立変数が従属変数に与える影響が、媒介変数を通じてどのように伝わるかを解析します。
- 確認的因子分析
- 事前に設定した因子構造に基づいてデータを検証する手法です。 観測変数が特定の因子にどのように関連するかを確認し、理論的なモデルの適合度を評価します。
- 多重指標モデル
- 潜在変数を複数の観測変数（指標）で測定し、その関係性を分析する方法です。 指標間の相関を考慮し、潜在変数の特性をより精度高く評価します。
2. パス図によるモデルの表現
変数間の関係を表すには、パス図を用います。 観測変数、潜在変数、誤差変数を四角形、楕円、円などの図形で表現し、各変数間（図形）を矢印でつなぐことで因果関係や相関関係を表現します。
構造方程式モデリングが実装された統計解析ソフトウェアでは、パス図を描くことでモデルを表現できるものが多く、 変数間の複雑な関係を簡潔に表現できます。
右図は、統計解析ソフトウェアStataで記述した構造方程式モデリングの一例です。
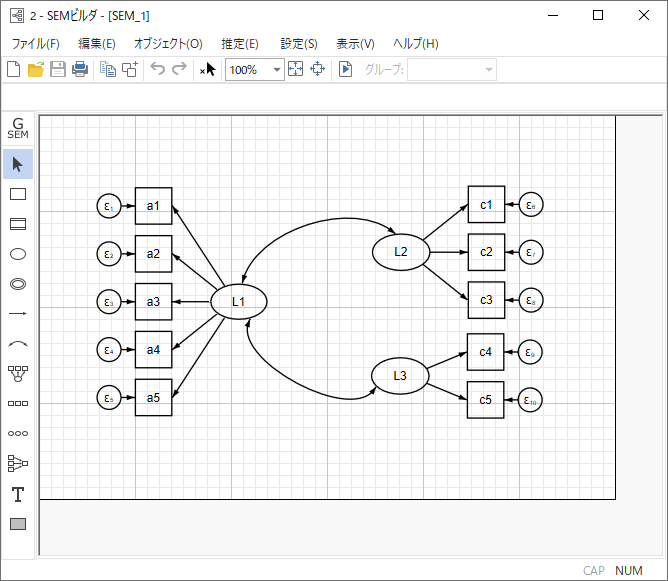
3. 多重指標モデル
多重指標モデルは、複数の観測変数（指標）を使用して、複数の潜在変数（因子）を測定するモデルです。 測定モデルと構造モデルの2つの主要な部分から構成されます。
- 測定モデル（Measurement Model）
- 潜在変数は直接観測できない概念（例：知能、満足度、社会的支援など）で、 観測変数はその潜在変数を示す実際のデータ（例：テスト結果、アンケートの項目、観察値など）です。 測定モデルでは、観測変数がどの潜在変数に関連しているか、そしてどれくらいの重み（因子負荷）を持つかを特定します。
- 構造モデル（Structural Model）
- 潜在変数間の因果関係を表現します。 変数がどのように相互に影響を与え合うかを示し、因果関係のパス（矢印） を定義することによって、変数間の関係を表現にします。
構造方程式モデリングにおける多重指標モデルは、複数の観測変数を使って潜在変数を測定し、これらの潜在変数間の関係を分析する方法です。 これにより、観測できない心理的な要因を考慮に入れつつ、因果関係をモデル化できるため、複雑なデータの解析に非常に強力なツールとなります。
4. 分析の流れ
構造方程式モデリングの分析手順は次のとおりです。
- 仮説に基づいて変数間の関係をモデル化する
- 構築したモデルをデータに当てはめる
- モデルがデータに適合しているか適合度を確認する
- 推定結果から考察を行う
- モデルの改善と再評価
モデルの適合度を評価するために、CFI（比較適合指数）、TLI（トール・ルイス指数）、RMSEA（平均二乗誤差）などの適合度指標を確認します。
初期のモデルが適合しない場合にモデルを修正することがありますが、理論的根拠を伴った変更を行うべきです。
5. まとめ
構造方程式モデリング（SEM）は、観測されたデータと潜在変数（直接観測できない概念）間の複雑な関係を明示化するための強力な分析手法です。
SEMでは、測定モデルと構造モデルを組み合わせることで、潜在変数間の因果関係を推定し、データの背後にある構造を解明できます。
これにより、心理学、社会学、マーケティングなどの分野で、消費者の態度や行動、企業の戦略的意思決定、健康状態の評価などを定量的に分析できます。
また、複数の指標を使用して、データ間の複雑な相互作用や因果関係を明示的に示すことができる点が大きな利点です。
構造方程式モデリング（共分散構造分析）ウェビナーのご案内
統計数理研究所の奥野先生を特別講師としてお招きし、構造方程式モデリングのウェビナーを開催します。
下記リンクより、詳細をご覧ください。
