回帰モデルで予測してみよう!
熱中症による搬送人員の予測を行うために回帰モデルを構築します。
単に回帰モデルといってもどの説明変数を使用するか、どのように変数を組合せるかによって予測結果は大きく変わります。
この分析では5つの回帰モデルを構築しましたが、1つ目に作成した回帰モデルと改良を重ねて精度を高めた回帰モデルでは、予測精度に大きな差が生じました。
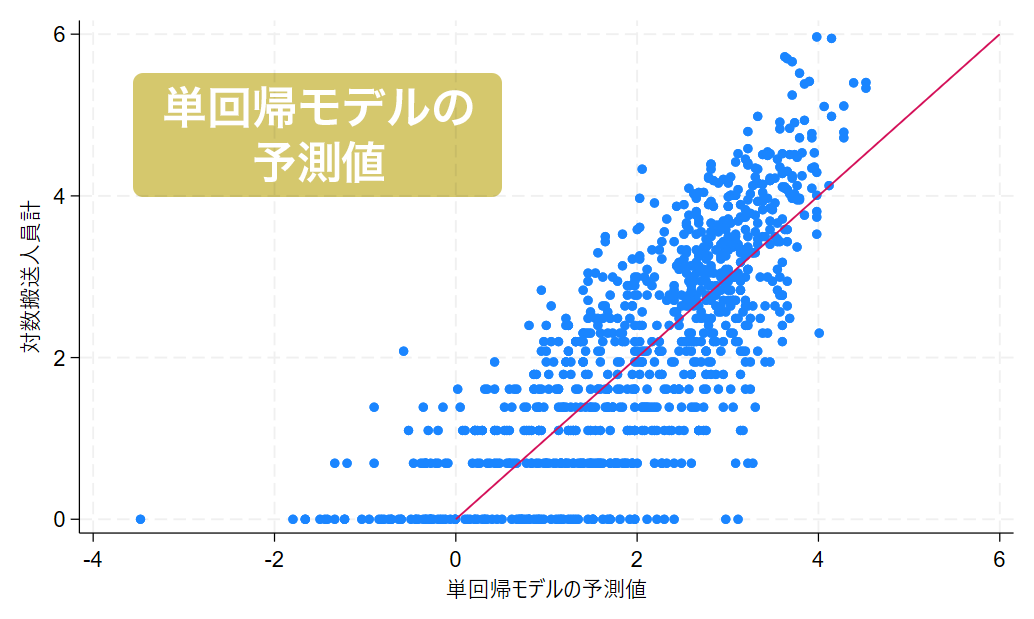
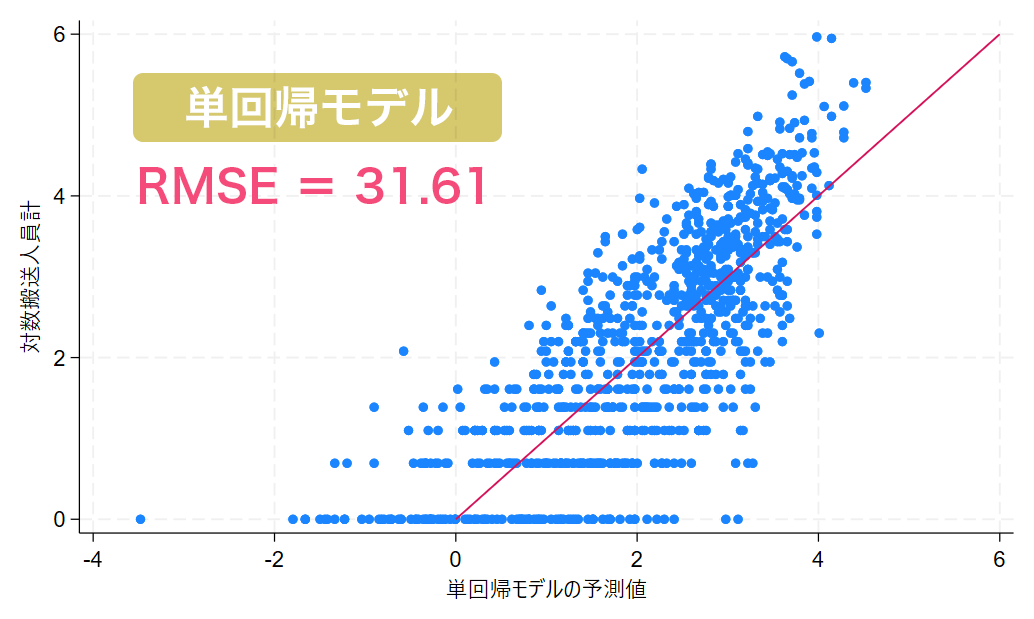
グラフは横軸を予測値、縦軸を実測値とし、予測値と実測値が等しいラインを赤線で表示しています。青いプロットが赤い直線付近にあるほど予測精度が高いことを意味します。
単回帰モデルのグラフでは、赤い直線に対して横軸が大きくなるほど上振れている点が多く、その範囲において予測値が過小であったといえます。
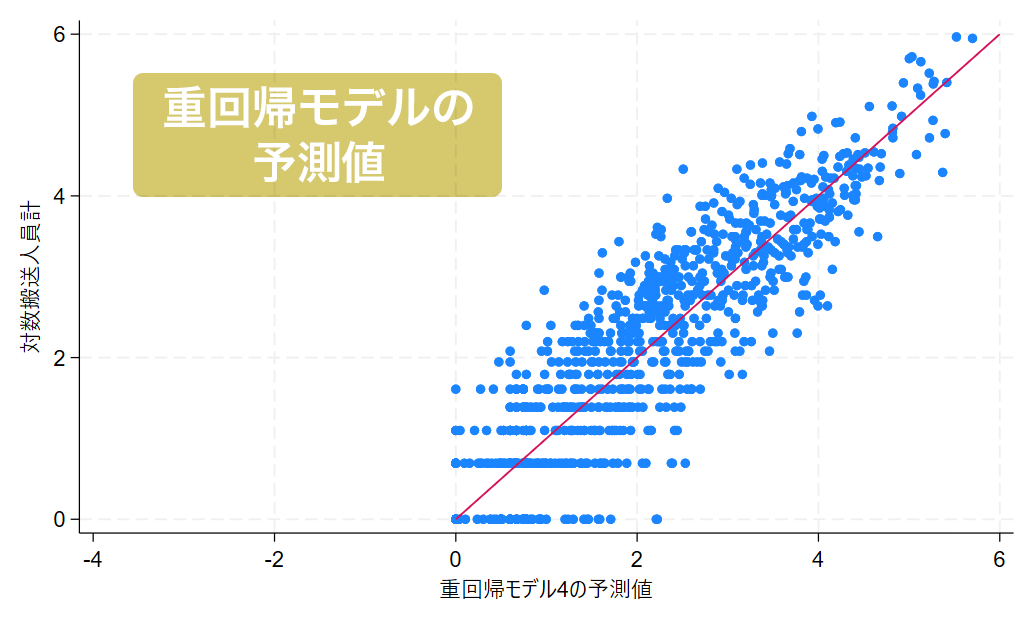
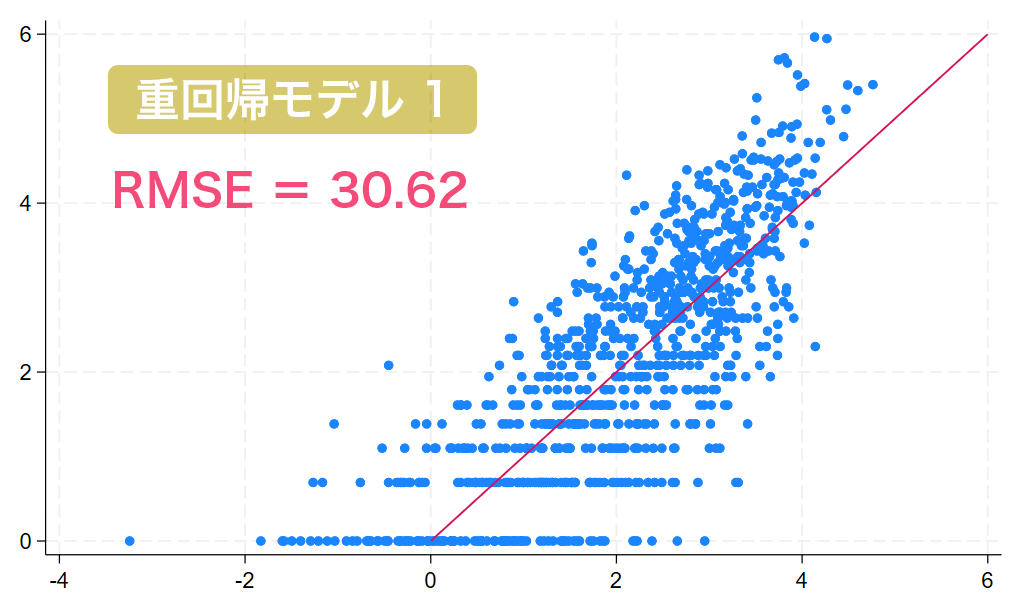
一方で、重回帰モデルのグラフでは赤い直線付近にプロットが集まっており、比較的良好な予測となっていることが視覚的にわかります。
回帰モデルをどのように構築するか、分析者によって考え方や手順は異なりますが、ここでは分析作業の一例をご紹介します。
どのように分析を行ってよいかわからない、分析作業は未経験でどのように着手すればよいか迷っている、といったお悩みを抱えている方はぜひご覧ください。
熱中症による搬送人員の予測

1. 予測分析の概要
今回の分析において、熱中症による搬送人員を高い精度で予測することを目的とします。
予測分析を行う上で熱中症情報と気象情報に関するオープンデータを総務省、国土交通省の各ホームページより取得しました。
分析に用いたデータの期間は、2018年から2022年の各年における5月から9月までの日次データです。
総務省消防庁のホームページにおいて公開されている熱中症情報では、日別都道府県別の搬送人員や年齢区分、傷病程度、発生場所に関する情報を入手できます。
国土交通省気象庁の気象データについては観測地点を選択してダウンロードすることができ、非常に多くの観測地点があることから地点を絞って活用しました。
具体的には、山形市、東京、名古屋市、大阪市、福岡市、那覇市の6地点におけるデータを使用しました。
予測と精度の検証について、2019年から2021年のデータを用いて回帰モデルを構築し、2022年の搬送人員を予測します。
2022年のデータにおける実測値と予測値の差を誤差(Error)とし、予測精度の評価指標としてRMSE(Root Mean Square Error)を用います。
RMSEは小さいほど実測値と予測値の差が小さく、精度の高い予測であることを意味します。

2. データの概要
データは複数のExcelファイルにて取得できますが、分析ソフトに読み込んで加工し、表形式のデータセットに整形します。
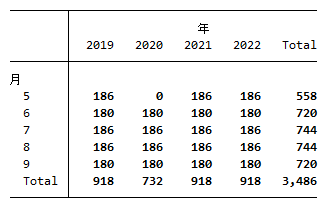
作成したデータセットは列数(変数の数)は32列、行数(観測数)は3,486行です。
年月別の観測数は表の通りですが、2020年5月の熱中症情報が掲載されていないため0行となっています。都市別の観測数は各都市561行です。

変数に関して日付と都道府県コードの2列の他、熱中症情報に関する変数が20列あり、熱中症情報の搬送人員計を予測対象の変数(目的変数)とし、その他の熱中症情報に関する列はその内訳となるためモデルにおいて使用しません。
また、気象情報に関する変数が10列あり、具体的な変数名(とその単位)は次の通りです。
平均気温(℃) 最高気温(℃) 最低気温(℃)
日照時間(時間) 平均風速(m/s)
合計全天日射量(MJ/㎡) 平均蒸気圧(hPa)
平均湿度(%) 降水量の合計(mm)
平均雲量(10分比)



次に、搬送人員計と気象情報の各変数との相関係数を示します。
搬送人員計がカウントデータであり、ヒストグラムで示した通り0に偏っているため、搬送人員計に1を加えて対数変換した変数である対数搬送人員計を用いました。
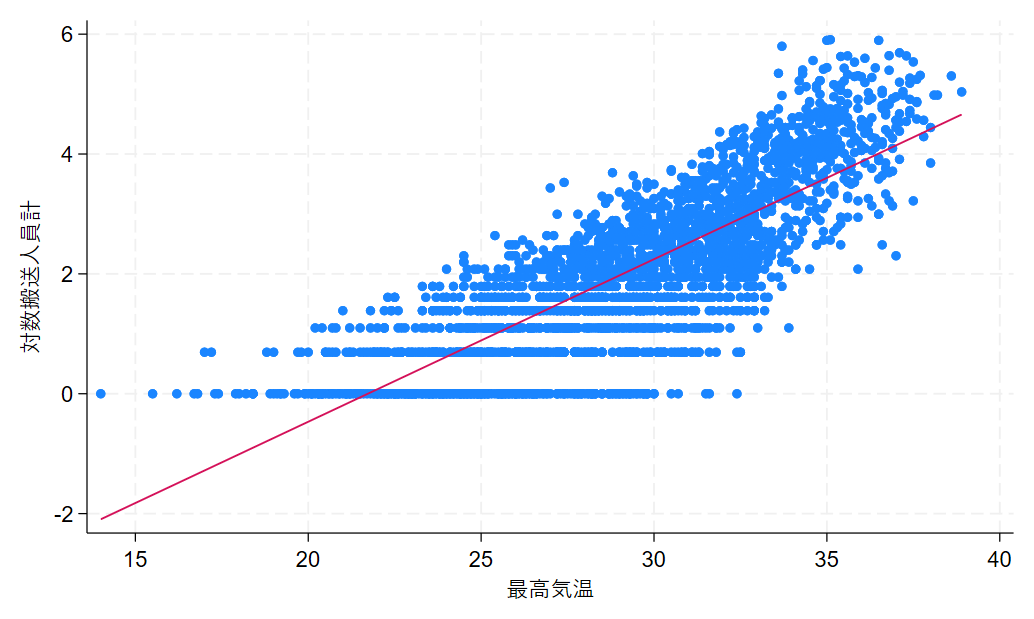
対数搬送人員計と最も相関の高い変数は最高気温であり、0.801でした。
| 対数搬送人員計 | |
|---|---|
| 対数搬送人員計 | 1.000 |
| 平均気温 | 0.698 |
| 最高気温 | 0.801 |
| 最低気温 | 0.560 |
| 日照時間 | 0.457 |
| 平均風速 | -0.145 |
| 合計全天日射量 | 0.461 |
| 平均蒸気圧 | 0.401 |
| 平均湿度 | -0.234 |
| 降水量の合計 | -0.252 |
| 平均雲量 | -0.316 |
3. 回帰モデルの構築と検証
単回帰モデル
対数搬送人員計と最も相関の高い最高気温を用いて単回帰モデルを推定しました。
推定には、2019年から2021年までのデータである2,568行を用いました。
自由度調整済み決定係数は0.6369でした。


次に、2022年のデータに対して推定した回帰直線を用いて対数搬送人員計の予測値を求めました。
予測値と実測値の散布図を掲載します。
赤線は予測値と実測値が等しくなる直線(y=x)であり、この直線付近にプロットが集中していることが望ましいといえます。
推定された回帰直線を用いて、2022年の対数搬送人員計を予測して指数変換した搬送人員計の予測値と実測値をもとに予測精度を算出した結果、RMSEは31.61でした。
以下では、回帰モデルを改良することで予測精度(RMSE)の改善を試みます。
重回帰モデル1
『3-1 単回帰モデル』では説明変数として最高気温のみを用いましたが、この単回帰モデルに説明変数を追加することにより、精度の高いモデルの構築を目指します。
どのような説明変数を組合せるべきかについては、データに対する深い知見が必要となりますが、ここでは暑さ指数(WBGT)という指標を参考にしました。
暑さ指数は熱中症を予防することを目的として1954年にアメリカで提案された指標です。
この暑さ指数を推定するための項目として、気温、湿度、気圧、全天日射量、平均風速などが利用されており、熱中症の搬送人員計を予測するために有効な変数であると予想されます。
そこで、これらの変数を説明変数として推定を行いました。
係数が5%有意とはならなかったものは除外するなど、説明変数を調整するために複数回の推定を行った結果、重回帰モデル1を得ました。
自由度調整済み決定係数は0.6645となり、単回帰モデルよりもあてはまりが良くなっています。
重回帰モデル2
『3-2 重回帰モデル1』では暑さ指数に使用されている項目を参考に変数選択を行いましたが、ここではステップワイズ法による変数選択を試みます。
ステップワイズ法は、回帰モデルを推定した後、あらかじめ設定した内容に基づいて説明変数を取捨選択して再度回帰モデルを推定します。
このモデル推定と変数の取捨選択の操作を繰返し行い、変数選択を行う手法です。
暑さ指数では考慮していなかった変数も含めて説明変数を検討することができます。
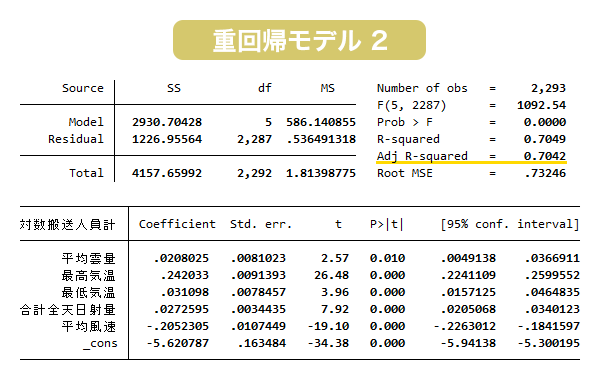
推定結果より、自由度調整済み決定係数は0.7042となり、重回帰モデル1よりも良いあてはまりでした。
重回帰モデル3
今回の分析では、6都府県におけるデータを使用していますが、各地域における人口にはばらつきがあります。
人口が多いほど搬送人員計が増えることは容易に想像できます。
そこで、回帰モデルに地域の情報を取り込むことを考えます。
具体的には、『3-2 重回帰モデル1』で用いた説明変数の係数を地域ごとに推定するようにモデルを修正します。
地域別に異なるパラメータを設定するため推定すべき係数の数が30と多くなりますが、観測数は2,568ですので問題ありません。
(観測数が少なく、パラメータ数を下回るような場合は、推定値が得られないため注意が必要です。)
推定結果より、自由度調整済み決定係数は0.9355であり、あてはまりが改善されました。
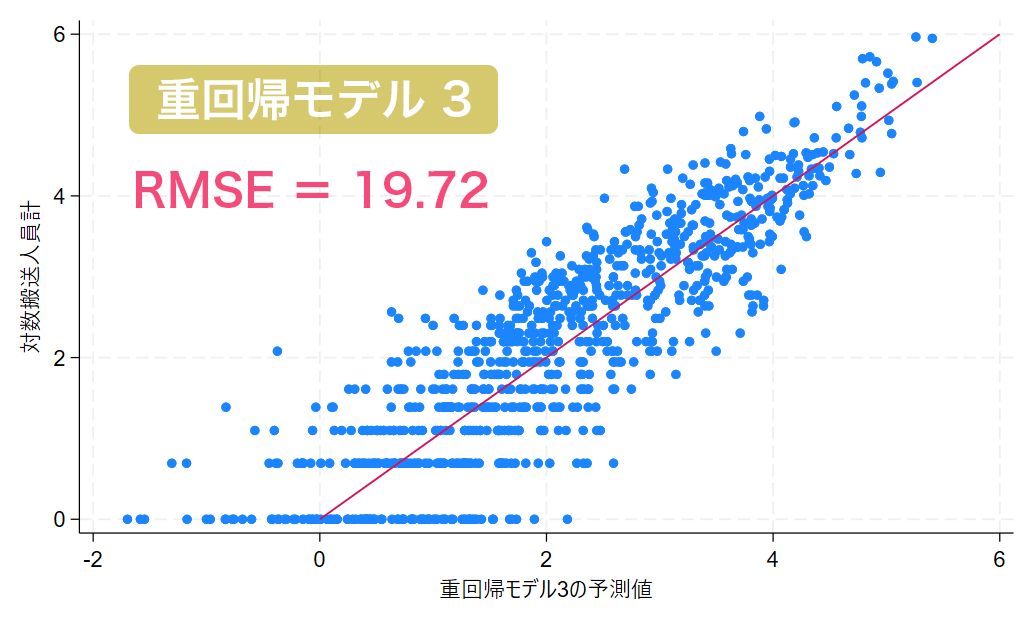
予測精度についてもRMSEが19.72となり、大きく改善されました。
『2. データの概要』で示した通り、搬送人員計のヒストグラムが都道府県別に異なっており、重回帰モデル3はこの点を適切にモデルに組み込んだことによって、予測精度の改善につながったと考えられます。
予測値と対数搬送人員計の散布図は次の画像となります。
グラフで確認すると、縦軸と横軸の値が等しい赤い直線(y=x)に近いプロットが増えています。
単回帰モデルの散布図と比較して予測精度が改善されていることが視覚的に確認できます。
対数搬送人員計が2以上の場合は比較的回帰直線まわりにプロットが集中している一方で、2以下の範囲においては値が小さくなるほど横方向のばらつきが大きくなっています。
このことから、重回帰モデル3による予測では、搬送人員計が0人や1人など少ない人数に対する予測が課題であり、『3-5 重回帰モデル4』ではこの点の改善を試みます。
重回帰モデル4
搬送人員計を予測する際に重要な説明変数として最高気温を採用しています。
重回帰モデル3では対数搬送人員計と最高気温が比例の関係であることを想定していますが、最高気温が低い日は搬送人員は少なくなる(0人または1人などのある一定の値に落ち着く)と考える方が自然なように思われます。
そこで、夏日であったか否かを示す変数(最高気温が25度以上の日を1、それ以外の日を0とする変数)として夏日フラグを生成し、夏日フラグを用いて前述の内容を表現するモデルを構築します。
推定結果より、自由度調整済み決定係数は0.9459であり、あてはまりが改善されました。
最高気温_夏日のみは最高気温と夏日フラグを掛け合わせた変数、日創時間_夏日のみも同様に日照時間と夏日フラグを掛け合わせた変数です。
予測値と対数搬送人員計の散布図を掲載します。
予測精度についてRMSEが18.62となり、改善されました。
重回帰モデル3では予測値(横軸)が-2に近い値をとるプロットもみられましたが、夏日フラグを導入した重回帰モデル4ではこの点が改善されていることがわかります。
4. まとめ
今回の分析では熱中症による搬送人員を高い精度で予測することを目的として回帰モデルを構築しました。
対数搬送人員計と最も相関の強い変数である最高気温を説明変数として用いた単回帰モデルをベースに暑さ指標を参考にした重回帰モデル、ステップワイズ法により変数選択を行ったモデル、その他変数を工夫して改良したモデルを構築しました。
訓練データに対するあてはまりの良さを確認する指標として自由度調整済み決定係数、予測の精度を示す指標としてRMSEを用いましたが、モデル毎の値の一覧は表の通りです。
| 自由度調整済み 決定係数 |
RMSE | |
|---|---|---|
| 単回帰モデル | 0.64 | 31.61 |
| 重回帰モデル1 | 0.66 | 30.62 |
| 重回帰モデル2 | 0.70 | 31.23 |
| 重回帰モデル3 | 0.94 | 19.72 |
| 重回帰モデル4 | 0.95 | 18.62 |
最も予測精度の高いモデルは重回帰モデル4でしたが、重回帰モデル4では下記の点を踏まえた回帰モデルとなっています。
- 暑さ指数を参考とした変数選択
- 都道府県ごとの係数の推定
- 夏日を考慮した変数の生成
熱中症による搬送人員計を高い精度で予測することを目的として分析を行いましたが、単回帰モデルを出発点として問題の背景を適切に捉え、それを回帰モデルに反映することで精度の高い回帰モデルを構築できました。