別に定めない限りFlexPDEは名称"T" （または"t"）を時間を表す変数と認識します。その時間への参照が定義項や方程式中に現れた場合、FlexPDEは初期値問題に適した解法を起動します。

FlexPDEは系の進展を追跡するために使用するタイムステップの制御にヒューリスティックスを用います。最初その値は変数の時間微分値に基づいて決められますが、その後変数の振舞いが2次関数的になるように調整されます。具体的に言うと、変数を時間についてテイラー級数に展開したとき、その3次の項がグローバルセレクタERRLIMの値よりも小さくなるようタイムステップを短くしたり伸ばしたりします。

時間依存型の問題の場合にはいくつか新たな項目を指定する必要があります。

時間帯については新たなセクション中で指定します。

TIME <start> TO <finish>

プロットを作成する時間値は該当するプロットコマンドに先行する形で指定します。指定様式としては特定の時間値をリストにして指定するか、あるいは時間間隔と終了時間を組み合わせて指定します。

FOR   T = <t1> <t2> BY <step> TO <t3> ...

ここでは時間依存型の問題例を示すために、これまで扱ってきた熱流体の方程式に時間依存項（右辺）を追加することにします。

Div(k*grad(Phi)) = c*dt(Phi)

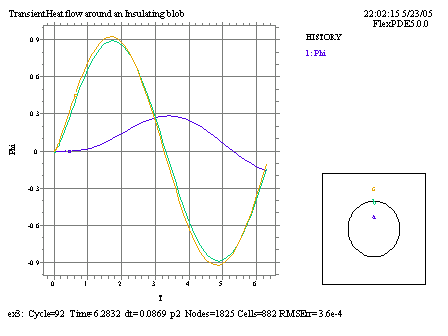
問題をより興味深いものとするために、上端のプレートの温度をsin(t)という形で変動させることにします。また内部の3点における温度変化をHISTORYプロットの形で出力させるコードも追加します。

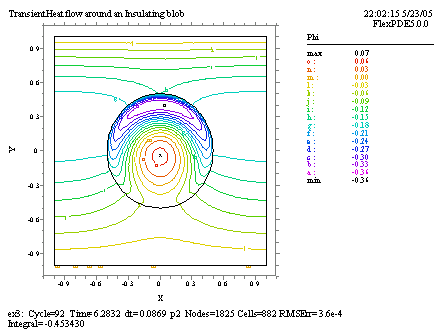
TITLE 'Transient Heat flow around an Insulating blob'

VARIABLES

Phi (threshold=0.01)        { the temperature }

DEFINITIONS

K = 1                { default conductivity }

C = 1                { default heat capacity }

R = 1/2

EQUATIONS

Div(-K*grad(phi)) + C*dt(Phi) = 0

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0          LINE TO (1,-1)

NATURAL(Phi)=0        LINE TO (1,1)

VALUE(Phi)=sin(t)     LINE TO (-1,1)

NATURAL(Phi)=0        LINE TO CLOSE

REGION 2        'blob'        { the embedded blob }

K = 0.001

C = 0.1

START(R,0)

ARC(CENTER=0,0) ANGLE=360

TIME 0 TO 2*pi

PLOTS

FOR T = pi/2 BY pi/2 TO 2*pi

CONTOUR(Phi)

VECTOR(-K*grad(Phi))

ELEVATION(Phi) FROM (0,-1) to (0,1)

HISTORIES

HISTORY(Phi) AT (0,r/2) (0,r) (0,3*r/2)

END

最終時点（t=2*pi）における等温線図、及びHISTORYプロットは次のようになります。