円柱座標を用いた例題

 先頭へ  前へ  次へ

 

 

先に用いた2次元直交座標系での問題を円柱座標系での問題に変換します。正方形領域（'box'）と円形領域（'blob'）を左端の境界を軸にして回転させると2つの円盤にはさまれたトーラスが形成されます。ただし次のような変更を加える必要があります。

 

•座標系をずらし、左端の境界がR=0となるようにする。
•回転軸を縦軸方向に取っているためYCYLINDER座標系を使用する。
•座標軸の名称として'R'が使用されることになるので、blobの半径としては別の名前を用いる。

 

このトーラスに対する問題を記述するスクリプトは次のようになります。

 

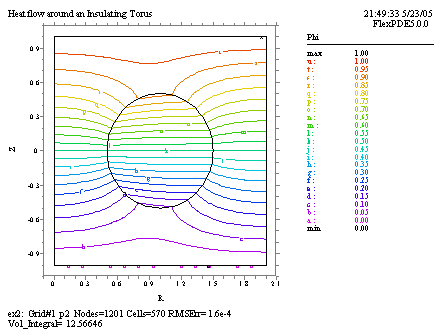
TITLE 'Heat flow around an Insulating Torus'

COORDINATES

YCYLINDER

VARIABLES

Phi                 { the temperature }

DEFINITIONS

K = 1               { default conductivity }

Rad = 0.5           { blob radius (renamed)}

EQUATIONS

Div(-k*grad(phi)) = 0

BOUNDARIES

REGION 1 'box'

START(0,-1)

VALUE(Phi)=0      LINE TO (2,-1)

NATURAL(Phi)=0    LINE TO (2,1)

VALUE(Phi)=1      LINE TO (0,1)

NATURAL(Phi)=0    LINE TO CLOSE

REGION 2        'blob'        { the embedded blob }

k = 0.001

START 'ring' (1,Rad)

ARC(CENTER=1,0) ANGLE=360 TO CLOSE

PLOTS

CONTOUR(Phi)

VECTOR(-k*grad(Phi))

ELEVATION(Phi) FROM (1,-1) to (1,1)

ELEVATION(Normal(-k*grad(Phi))) ON 'ring'

END

 

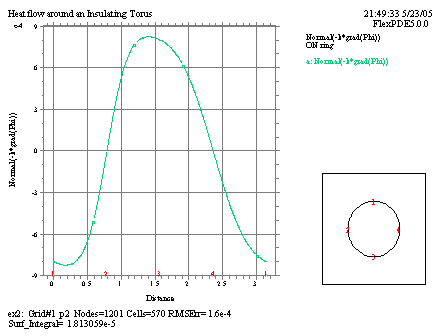
ここでは出力結果のうち、等温線図と境界上での法線方向熱流束の図を示しておきます。

 

ex201_001

 

ex204_001