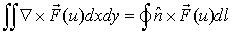部分積分は数学上の基本操作の一つであるため、その適用が数多くの基本的物理法則(例えばアンペールの法則)につながっていたとしても驚くには当たりません。
このため自然境界条件は多くの応用分野における基本的な保存則を記述することになる場合がしばしばあります。
しかしラプラス方程式よりも複雑な方程式においてはその意味が常に自明であるとは限りません。
そこでまずいくつかの基本的な項とその自然境界条件による寄与を見て行くことにしましょう(ここでは2次元の場合について述べますが、3次元への拡張も容易に行えます)。
| • | 項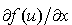 に部分積分を適用すると に部分積分を適用すると
|
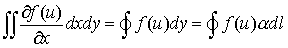
が導かれます。ここに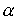 は境界線上の法線のx方向余弦、 は境界線上の法線のx方向余弦、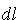 は微小径路長を表します。FlexPDEは部分積分を2階微分の項にしか適用しないので、この公式は関数 は微小径路長を表します。FlexPDEは部分積分を2階微分の項にしか適用しないので、この公式は関数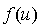 にさらに にさらに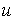 の導関数が含まれている場合にのみ適用されます。x以外の座標変数に対しても同様です。 の導関数が含まれている場合にのみ適用されます。x以外の座標変数に対しても同様です。
| • | 項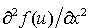 に部分積分を適用すると に部分積分を適用すると |
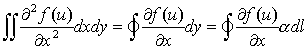
が導かれます。この項は2階微分であるため、常に自然境界条件への寄与項が導かれます。
| • | 項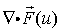 に部分積分を適用すると発散定理 に部分積分を適用すると発散定理 |
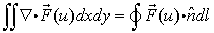
が導かれます。ここに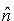 は境界上の外向き単位法線ベクトルを表します。最初の例の場合と同様、ベクトル は境界上の外向き単位法線ベクトルを表します。最初の例の場合と同様、ベクトル 自身にuの導関数が含まれていない場合には部分積分は適用されません。 自身にuの導関数が含まれていない場合には部分積分は適用されません。
| • | 項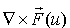 に部分積分を適用すると回転定理 に部分積分を適用すると回転定理 |
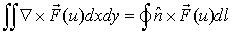
が導かれます。
これらの公式を用いて自然境界条件の意味をチェックしておきましょう。
熱拡散方程式
Div(-k*grad(Temp)) + Source = 0
Natural(Temp) = 外向き法線方向流束 = normal(-k*grad(Temp))
Note:
|
偏微分方程式中、熱流束に対しては負の符号を付してある点に注意してください。この符号を付けなかった場合にはNaturalの指定も反転させる必要があります。
|
1次元熱拡散方程式
dx(-k*dx(Temp)) + Source = 0
Natural(Temp) = 流束の外向き法線成分 = (-k*dx(temp)*nx)
ただしnxは境界上の法線のx方向余弦。x以外の座標変数に対しても同様。
磁場方程式
curl(curl(A)/mu) = J
Natural(A) = Hの接線方向成分 = tangential(curl(A)/mu)
対流方程式
dx(u)-dy(u)=0
2階の項がないためNatural(u)は定義されない。
|
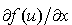 に部分積分を適用すると
に部分積分を適用すると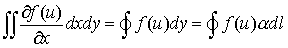
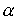 は境界線上の法線のx方向余弦、
は境界線上の法線のx方向余弦、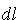 は微小径路長を表します。FlexPDEは部分積分を2階微分の項にしか適用しないので、この公式は関数
は微小径路長を表します。FlexPDEは部分積分を2階微分の項にしか適用しないので、この公式は関数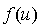 にさらに
にさらに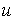 の導関数が含まれている場合にのみ適用されます。x以外の座標変数に対しても同様です。
の導関数が含まれている場合にのみ適用されます。x以外の座標変数に対しても同様です。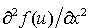 に部分積分を適用すると
に部分積分を適用すると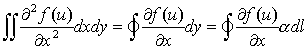
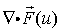 に部分積分を適用すると発散定理
に部分積分を適用すると発散定理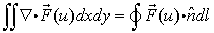
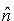 は境界上の外向き単位法線ベクトルを表します。最初の例の場合と同様、ベクトル
は境界上の外向き単位法線ベクトルを表します。最初の例の場合と同様、ベクトル 自身にuの導関数が含まれていない場合には部分積分は適用されません。
自身にuの導関数が含まれていない場合には部分積分は適用されません。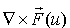 に部分積分を適用すると回転定理
に部分積分を適用すると回転定理