|
|
自然境界条件という用語は通常変分法の中で用いられます。しかし有限要素法も本質的には誤差汎関数(functional)を最小化するものであることから、この用語は有限要素法との兼ね合いにおいても使用されます。
しかしこの用語に対してはより直感的でわかりやすい意味付けも可能です。
ラプラスの方程式
について考えてみましょう。発散定理によれば左辺の量を平面領域A上で面積分した値は流束の法線方向成分を境界線上で線積分した値に等しくなります。
(これは2次元の式ですが、3次元でも同様のことが言えます。)
境界上での値
発散定理はより一般的な部分積分公式
の姿を変えたものと見ることもできます。
項
FlexPDEは偏微分方程式中でシステム変数の2階微分を含むすべての項にこの部分積分公式を適用します。もちろんラプラス方程式の場合にはすべての項がこれに該当するわけです。
ラプラス方程式の解を求めるためには、境界上のすべての点において変数(
FlexPDEの記法で言うと、
言い換えるなら
FlexPDEにおける自然境界条件は境界面/境界線上での流束の値を指定します。その流束は偏微分方程式の部分積分によって規定されるものでもあります。 流束の値は非線形なものでも構いません。
例えば熱せられた物体からの放射損失は温度の4乗に比例します。従って次のステートメント
NATURAL(u) = -k*u^4
はラプラス方程式の境界条件として全く妥当なものと言えます。
|
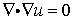
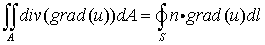
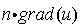 は実はラプラス(およびポアッソン)方程式の自然境界条件でもあります。これは境界内部の系が外部の系とどうインタラクトするかを示すものです。すなわち系の境界を横切るuの流れ(の符号を反転させたもの)の量を表しています。
は実はラプラス(およびポアッソン)方程式の自然境界条件でもあります。これは境界内部の系が外部の系とどうインタラクトするかを示すものです。すなわち系の境界を横切るuの流れ(の符号を反転させたもの)の量を表しています。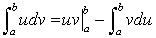
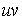 を積分境界上で評価することによって境界上の積分式が出てきます。divergenceの積分にこの公式を適用することによって発散定理の式が導かれます。
を積分境界上で評価することによって境界上の積分式が出てきます。divergenceの積分にこの公式を適用することによって発散定理の式が導かれます。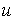 )の値を指定するか
)の値を指定するか