レイヤ境界の変形

 先頭へ  前へ  次へ

 

 

先にレイヤ境界は平面に限らないと述べました。しかしFlexPDEはレイヤ境界に対しある種の仮定を置いているため、設定できる形状には多少制約が付きます。

 

•3次元オブジェクトは側面とレイヤ境界を持ち、extrudeされた形状を維持したものでなくてはならない（側面はのばしたり縮めたりすることはできない）。
 
•レイヤ境界面はリージョン境界をまたがって連続でなくてはならない。垂直なジャンプを伴う境界面の場合、それは複数のレイヤに分ける必要がある。その際、ジャンプはリージョン境界で発生するものとし、個々のレイヤはジャンプの両側にまたがる形で設定する（jumpではなくlayers）。
 
•境界面同士はマージしても良いが、逆転することがあってはならない。（上下の）逆転を防ぐためには面の定義においてMAX, MIN関数を使用すると良い。
 

これらのルールに従ってキャニスターを球（上下の半球からなる）に変更してみましょう。
 

半球面を与える数式としては次のいずれかが使用できます。

 

Z = Zcenter + sqrt( R^2 – x^2 – y^2)
 

または
 

Z = Ztop – R + sqrt(R^2 – x^2 – y^2)

 

•全体をカバーする直方体の上面、下面にこれら半球が接触することを回避するために、extrusionの範囲を-1から1まで拡張します。
 
•計算時のエラーを防ぐため、sqrt中の引数は負にならないように工夫をします。

 

新たなスクリプトは次のようになります。

 

TITLE 'Heat flow around an Insulating Sphere'

COORDINATES

Cartesian3

VARIABLES

Phi                { the temperature }

DEFINITIONS

K = 1              { default conductivity }

R = 0.5            { sphere radius }

{ shape of hemispherical cap: }

Zsphere = sqrt(max(R^2-x^2-y^2,0))      

 

EQUATIONS

Div(-k*grad(phi)) = 0      

 

EXTRUSION

SURFACE 'Bottom'  z=-1

LAYER 'underneath'

SURFACE 'Sphere Bottom'  z = -max(Zsphere,0)

LAYER 'Can'

SURFACE 'Sphere Top'  z = max(Zsphere,0)

LAYER 'above'

SURFACE 'Top'         z=1

 

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0          LINE TO (1,-1)

NATURAL(Phi)=0        LINE TO (1,1)

VALUE(Phi)=1          LINE TO (-1,1)

NATURAL(Phi)=0        LINE TO CLOSE

LIMITED REGION 2        'blob'        { the embedded blob }

LAYER 2 K = 0.001

START 'ring' (RSphere,0) ARC(CENTER=0,0) ANGLE=360

TO CLOSE

PLOTS

GRID(y,z) on x=0

CONTOUR(Phi) on x=0

VECTOR(-k*grad(Phi)) on x=0

ELEVATION(Phi) FROM (0,-1,0) to (0,1,0)

END

 

左側の図は上半分から外周部を取り去ったもの、右側の図は平面x=0による切断面です。

 

3ex4c00   3ex4a00

 

 

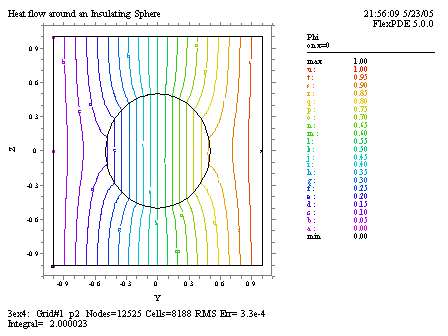
等温線図は次のようになります。

 

 

3ex402_001

 

対象とした3次元オブジェクトの対称性から、このプロットは2次元の等温線図を回転させたものと類似の形状となっています。