3次元における積分

 先頭へ  前へ  次へ

 

 

3次元の問題の場合、リージョンとレイヤとによって選択された3次元区画（volume compartments）上で体積積分が実行できます。

 

•Result = VOL_INTEGRAL(<integrand>)

ドメイン全体を対象にintegrandの積分を計算します。

 

•Result = VOL_INTEGRAL(<integrand>, <region name>)

指定されたリージョン内の全レイヤを対象にintegrandの積分を計算します。

 

•Result = VOL_INTEGRAL(<integrand>, <layer name>)

指定されたレイヤ内の全リージョンを対象にintegrandの積分を計算します。

 

•Result = VOL_INTEGRAL(<integrand>, <region name>, <layer name>)

リージョン名、レイヤ名で規定される3次元区画を対象にintegrandの積分を計算します。

 

•Result = VOL_INTEGRAL(<integrand>, <region number>, <layer number>)

リージョン番号、レイヤ番号で規定される3次元区画を対象にintegrandの積分を計算します。

 

選択された面上で面積分が実行できます。種々の修飾詞名を解析することにより、FlexPDEは面積分のステートメントでどの面が対象かを推定します。平面ではなかった場合には実際の表面積によって重み付けが行われます。

 

•Result = SURF_INTEGRAL(<integrand>)

ドメインの外周を形成する面上でintegrandの積分を計算します。

 

•Result = SURF_INTEGRAL(<integrand>, <surface name> [, <layer_name>] )

指定されたextrusion面に含まれる全リージョン上でintegrandの積分を計算します。オプショナルなレイヤ名によってレイヤを特定することもできます。

 

•Result = SURF_INTEGRAL(<integrand>, <surface name>, <region name> [, <layer_name>] )

指定されたextrusion面のうち特定のリージョンに範囲を限定してintegrandの積分を計算します。オプショナルなレイヤ名によってレイヤを特定することもできます。

 

•Result = SURF_INTEGRAL(<integrand>, <region name>, <layer name>)

リージョン名、レイヤ名で規定される3次元区画のすべての面を対象にintegrandの積分を計算します。値の評価は3次元区画内を前提に行われます。

 

•Result = SURF_INTEGRAL(<integrand>, <boundary name> [, <region_name>] )

指定された基盤平面上の曲線をextrudeすることによって生成される側面に含まれるすべてのレイヤを対象にintegrandの積分を計算します。オプショナルなリージョン名が指定された場合には、それはどちらの表面を対象に積分計算を行うかを規定します。指定されたレイヤに隣接しない面は計算の対象とはなりません。

 

•Result = SURF_INTEGRAL(<integrand>, <boundary name>, <layer name> [, <region_name>] )

指定された基盤平面上の曲線をextrudeすることによって生成される側面のうち指定されたレイヤの部分を対象にintegrandの積分を計算します。オプショナルなリージョン名が指定された場合には、それはどちらの表面を対象に積分計算を行うかを規定します。指定されたレイヤに隣接しない面は計算の対象とはなりません。

 

Note:

これらの積分の用例については "Samples | Misc | 3D_Integrals.pde" を参照してください。

 

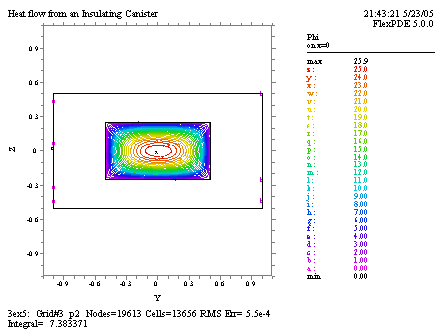
ここではキャニスターの問題に熱源を加え、その熱量の体積積分値を流束の面積分値と対比させます。これによって解の精度がチェックできます。

 

TITLE 'Heat flow from an Insulating Canister'

COORDINATES

Cartesian3

VARIABLES

Phi                { the temperature }

DEFINITIONS

K = 1          { default conductivity }

R = 0.5        { blob radius }

S = 0

EQUATIONS

Div(-k*grad(phi)) = S

EXTRUSION

SURFACE 'Bottom'        z=-1/2

LAYER 'underneath'

SURFACE 'Can Bottom'    z=-1/4

LAYER 'Can'

SURFACE 'Can Top'       z=1/4

LAYER 'above'

SURFACE 'Top'           z=1/2

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0          LINE TO (1,-1)

NATURAL(Phi)=0        LINE TO (1,1)

VALUE(Phi)=1          LINE TO (-1,1)

NATURAL(Phi)=0        LINE TO CLOSE

REGION 2        'blob'     { option: could be LIMITED }

LAYER 2 k = 0.001        { the canister only }

S = 1                    { still the canister }

START 'ring' (R,0)

ARC(CENTER=0,0) ANGLE=360 TO CLOSE

PLOTS

GRID(y,z) on x=0

CONTOUR(Phi) on x=0

VECTOR(-k*grad(Phi)) on x=0

ELEVATION(Phi) FROM (0,-1,0) to (0,1,0)

 

SUMMARY

REPORT(Vol_Integral(S,'blob','can')) AS 'Source Integral'

REPORT(Surf_Integral(NORMAL(-k*grad(Phi),'blob','can')))

AS 'Can Heat Loss'

REPORT(Surf_Integral(NORMAL(-k*grad(Phi))))

AS 'Box Heat Loss'

REPORT(Vol_Integral(S,'blob','can')-Surf_Integral(NORMAL(-k*grad(Phi))))

AS 'Energy Error'

END

 

等温線図は次のようになります。

 

3ex502_001

 

サマリページは積分計算の結果を示しています。

 

3ex505

Note:

等温線図下部に表示されている積分値はプロットプロセスがデフォルトで計算する Area_Integral(Phi) の値を示しています。