2つの伝導体間の接触抵抗の問題はモデル変数の不連続性を伴う典型例です。

この問題の場合、非常に薄い抵抗層が境界の両側で温度や電位のジャンプを引き起こします。ジャンプの大きさは抵抗層を横切る熱流や電流に比例します。顕微鏡で見れば抵抗物質に物理的広がりがあるわけですが、有限要素法モデルで忠実にモデル化し得るだけの厚みがあるわけではありません。

接触抵抗の場合、材質 '1' と '2' の間の抵抗層を横切る熱流束は '1' の側から見て

F1 = -K1*dn(T) = -(T2-T1)/R

と定式化されます。ここに

を意味します。

一方、'2' の側から見たときは

F2 = -K2*dn(T) = -(T1-T2)/R = -F1

となります。法線は逆の符号を持つため '2' からの流れは '1' からの流れの符号を反転させたものとなります（エネルギー保存）。

熱拡散方程式

div(-K*grad(T)) = H

の自然境界条件は発散定理より外向き熱流束を表す

Natural(T) = -K*dn(T)

で与えられます。

NATURAL の代りに CONTACT 境界条件を使用することにより、この熱流束を不連続変数と関係付けることができます。

FlexPDEにおける表現 JUMP(T) は材質 '1' 中では (T2-T1) と、材質 '2' 中では (T1-T2) と定義されます。従って接触抵抗の境界条件は次のように表されます。

CONTACT(T) = -JUMP(T)/R

このステートメントは境界をシェアする双方の材質において同じことを意味します。（JUMPに付された符号は発散項の符号を反映したものです。）

これまでの例にジャンプを引き起こす熱源を加えた形でスクリプトを変更してみましょう。なお、正方形領域の4辺とも今回は温度0に保つものとします。

TITLE 'Contact Resistance on a heated blob'

VARIABLES

Phi                { the temperature }

DEFINITIONS

K = 1          { default conductivity }

R = 0.5        { blob radius }

H = 0          { internal heat source }

Res = 0.5      { contact resistance }

EQUATIONS

Div(-k*grad(phi)) = H

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0        { cold outer walls }

LINE TO (1,-1) TO (1,1) TO (-1,1) TO CLOSE

REGION 2        'blob'        { the embedded blob }

H = 1        { heat generation in the blob }

START 'ring' (R,0)

CONTACT(phi) = -JUMP(phi)/Res

ARC(CENTER=0,0) ANGLE=360 TO CLOSE

PLOTS

CONTOUR(Phi)

SURFACE(Phi)

VECTOR(-k*grad(Phi))

ELEVATION(Phi) FROM (0,-1) to (0,1)

ELEVATION(Normal(-k*grad(Phi))) ON 'ring'

END

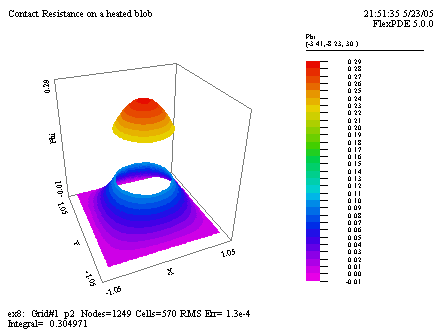
FlexPDEによって出力された曲面（surface）プロットには温度の不連続性が明確に表現されています。