計量経済分析ソフトウェア EViewsによる経済予測2
予測の評価と改善
第一回は予測の基本的な考え方と、EViewsでの基本的な手順について解説しました。第二回は第一回の内容を拡張し、予測の評価と予測の改善について解説します。
第二回の内容は以下の通りです。
予測の評価
第一回では予測の難しさについて解説しました。その中で、静的予測のほうが動的予測よりもフィットが良くなっていました。予測精度を統計的に評価するには、予測評価機能を用います。 操作を省略するため、静的予測と動的予測を実行するプログラムcont.prgをご用意しましたので、macromod.wf1で実行してください。cont.prgは以下のようなプログラムです。
equation eqcont.ls d(gdp) c @trend ar(1) ar(2) ma(1)
smpl 1960 2005
eqcont.forecast(e, g) gdp_dynamic
eqcont.fit(e, g) gdp_static
group groupcont gdp gdp_dynamic gdp_static
show groupcont.line
その後、gdpを開き、View > Forecast Evaluationと操作します。ダイアログに以下のように入力します。
結果が表示されます。複数の指標が用意されておりますが、ここでは最後のEvaluation Statisticsにご注目ください。すべての統計指標でGDP_Staticの値が小さくなっており(灰色のバックグラウンドで表示されます)、静的予測の方が精度が高いことが数字で確認できました。
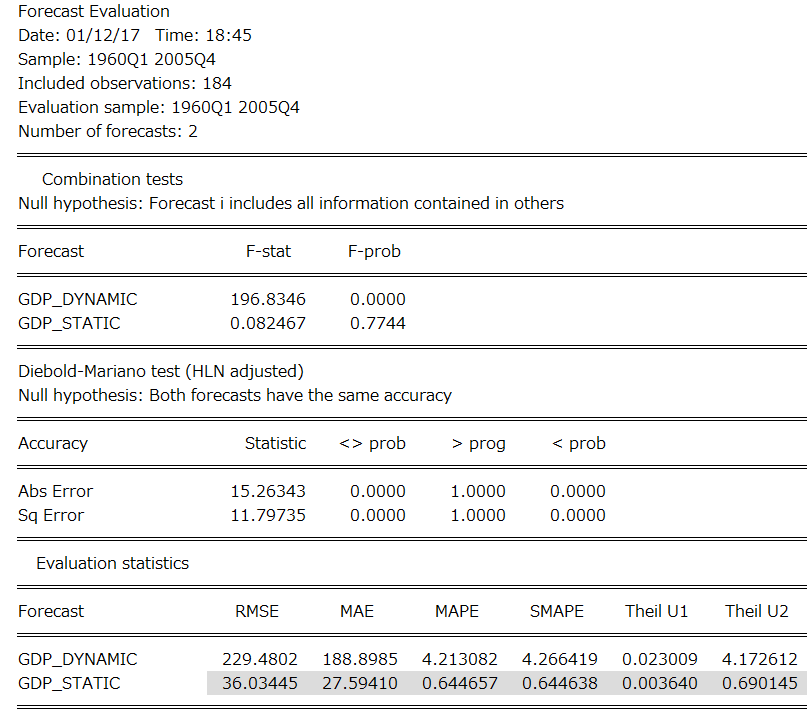
予測評価は、静的予測vs動的予測のケースだけに限らず、より一般的なケースで利用できます。例えば異なる説明変数セットを用いた場合の予測値を比較するなどです。また、各予測値を評価するのではなく、平均化して新しい予測値を算出することも可能です。これについては、別のページにて詳しく解説しておりますので、そちらをご覧ください。
予測の改善
予測値と実現値の比較や、上で解説した予測評価を行った結果、予測精度に満足できなかったとします。このような場合、以下のように推定を見直すことが考えられます。
説明変数を増やす
説明変数を増やすことは、モデルの説明力を高める上で非常に有力な選択肢です。しかしながら、第一回で説明したように、説明変数を増やすと予測の際に困難が生じます。もちろん、その説明変数が予測モデルにとってどうしても必要であれば利用するべきですが、まずは予測計算を阻害しない変数を追加して予測を行い、フィットが改善するかを確認するのが実務的な対応と言えるのではないでしょうか。予測計算を阻害しない変数とは、例えば以下のようなものです。
- 定数項…c
- トレンド項…@trend
- ar項、ma項、sar項、sma項…ar()、ma()、sar()、sma()
- 季節ダミー…@seas()
- 時点ダミー…@before、@after、@during
これらはEViewsによって自動で補われますので、予測値計算を阻害しません。例えば以下のような推定例を考えてみます。
d(gdp) c @trend ar(1) ar(2) ma(1) sar(4) sma(4) @seas(1)@seas(2) @seas(3) @after("1991q1")
元々の式と比べ、以下の変数が追加されています。
- sar(4) sma(4)で、4次の季節AR(Seasonal AR)項、季節MA項(Seasonal MA)項を追加しています。他にAR項、MA項がない場合、AR(4)とSAR(4)、MA(4)とSMA(4)は同値ですが、他にAR項やMA項がある場合は取扱いが異なります。詳しくはEViews Users Guide2(英文マニュアル)内の、“Seasonal ARMA Terms”をご確認ください。
- @seas(1)、@seas(2)、@seas(3)はそれぞれ、Q1、Q2、Q3についての時点ダミーです(なお、完全な多重共線関係になるのを避けるため、Q4を同時に含めることはできません)。月次データの場合、1~12までの値を指定することで、月次ダミーを設定することが可能です。例えば、データの季節変動を上手く説明できていないような場合に利用することが考えられます。
- @after("1991q1")で1991q1以降に1を取るダミーを追加しています。時点を" "で囲う必要があります。@duringの場合は、@during("1991q1 1995q2")のように始期と終期を半角スペース区切りで指定します。例えば、構造変化がある場合や、景気後退期のダミーを作りたいような場合に利用を検討することが考えられます。
グラフ化してみると、緑で表される修正版予測値は、赤で表される修正前予測値とそれほど異なっているようには見えません。
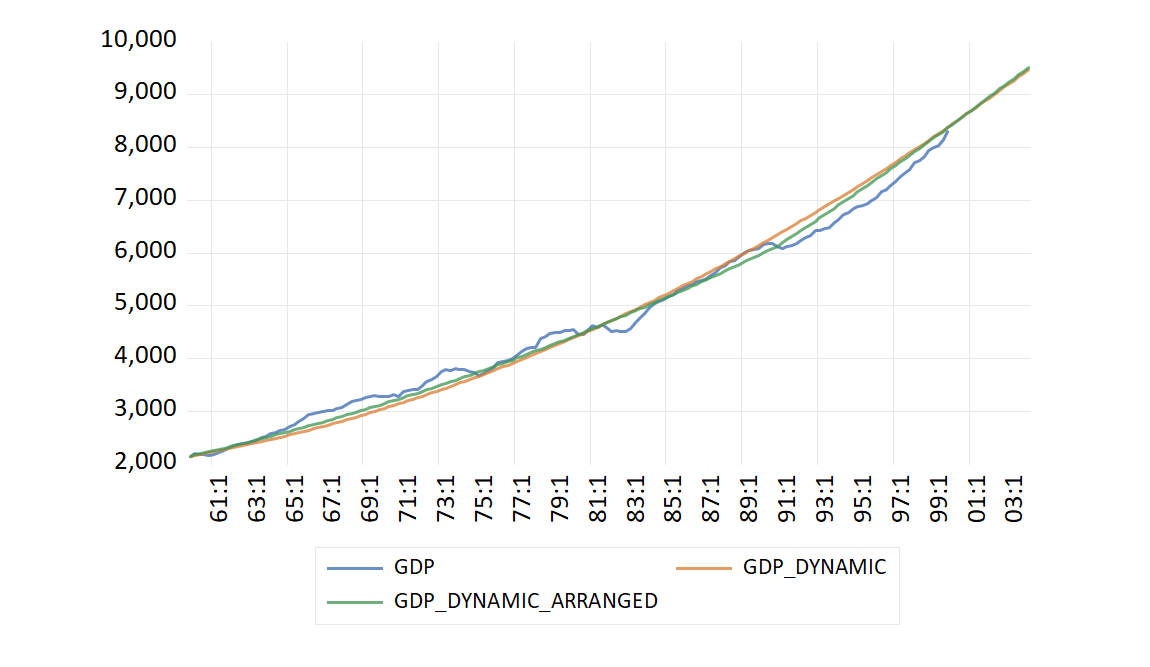
しかしながら、1991年以降に関しては、緑の修正版予測値の方が青い実現値に近づいています。これにはおそらく、「1991年q1以降ダミー」が関係していると推測されます。ただし気になるのは、緑と赤の値が段々近づいていき、最終的には逆転することです。予測の本番はあくまで2000年Q1以降なわけですから、上で追加した変数が真の予測において良い結果をもたらすか否かは慎重に判断する必要があります。このように、説明変数は増やせばよいというわけではありません。
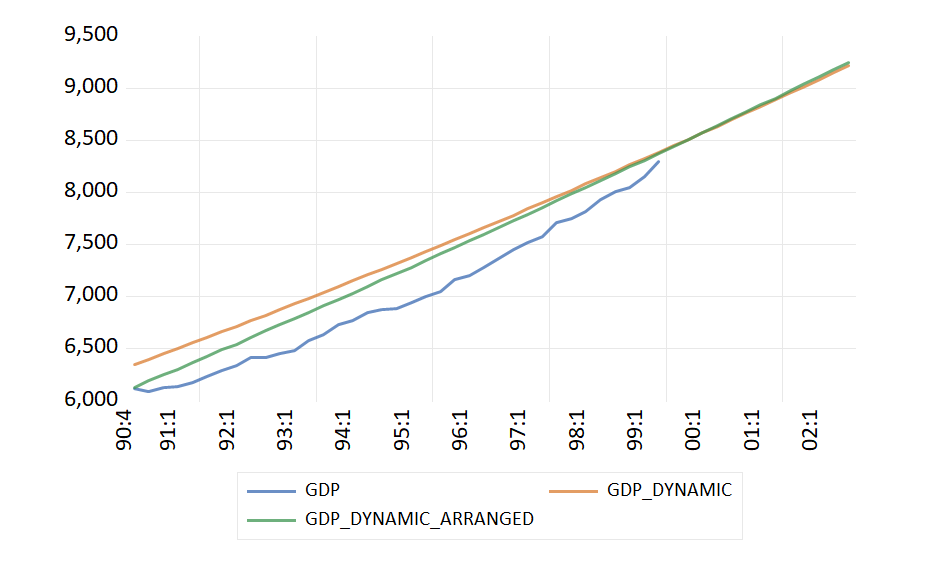
ARIMA次数の取り方を再考する
ARIMA次数の指定が良くない可能性も考えられます。これまではARMA項を恣意的に指定してきましたが、EViewsの機能である、“Automatic ARIMA Forecasting”を用いると、統計的基準に基づいてARIMAモデルを自動選択することが可能です。gdpを開き、ProcメニューよりAutomatic ARIMA Forecastingを選択します。赤で囲った場所を変更します(AR項やMA項の最大次数を指定し、その範囲で最適なモデルを検索します)。
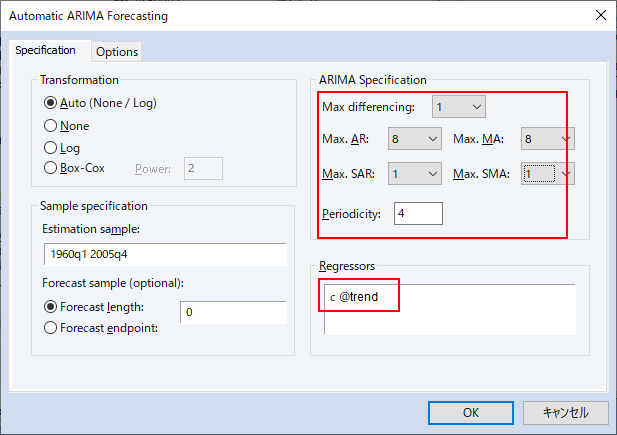
Optionsタブでは、モデル選択に利用する統計指標や、出力するアウトプットを選択できます。初期状態ではAkaike Information Criterion(赤池情報量基準、AIC)が選択されています。AICは予測に基づいてモデル選択を行うための指標ですので、ここではそのままにします。Equation output tableにチェックを入れます。
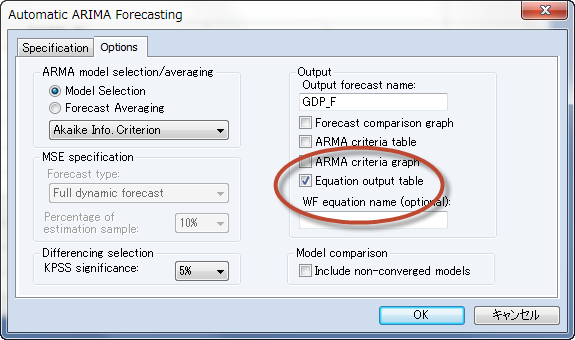
OKを押して実行します。最尤法による推定を何度も行い、その中から最適なモデルを選びますので、実行には少々時間がかかります。
基本結果は以下のように表示されます。Selected dependent variableが DLOG(GDP)になっていることにご注目ください。これまでのように、d()で階差を取るのではなく、dlog()で対数階差を取ったほうが良いという判定がなされました。また、Selected ARMA modelは(4, 3)(0, 1)と表示されました。これはそれぞれ、(AR項、MA項)(SAR項、SMA項)の最大次数に対応します。
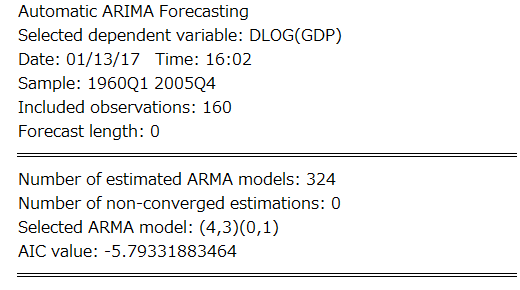
上の基本結果を元に、新しく推定し直すのが基本的な利用方法です。しかしこの場合、Equation output tableにチェックを入れていたので、上記のモデルの推定結果が続けて表示されます。
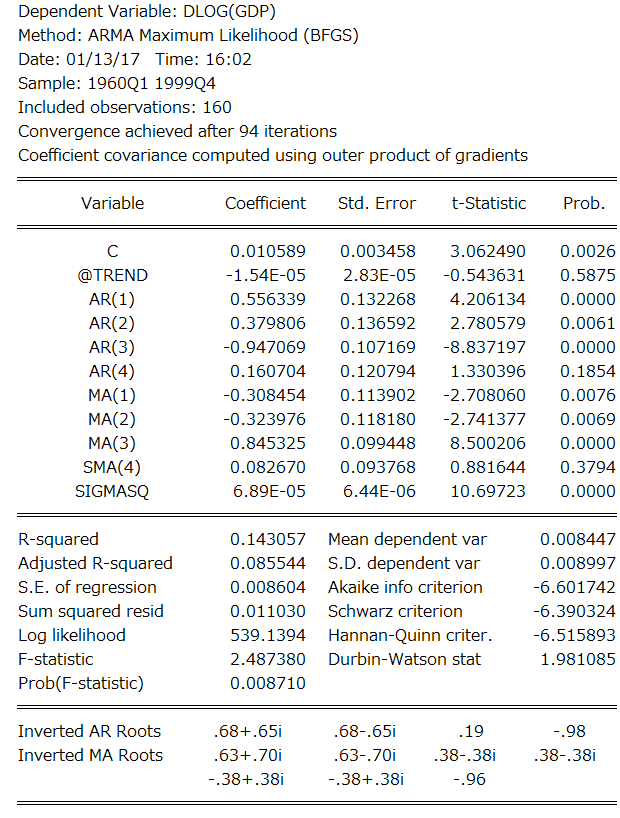
ARIMAモデルを使って予測する際は、項数を恣意的に決めるのではなく、本機能を用いて決めるとよいでしょう。
まとめ
今回は予測の評価と改善について解説しました。予測の改善については予測の簡便性を損なわない方法を解説しましたが、説明変数を追加しないと大きく進展しないような場合も多々あります。その場合、VARやモデルオブジェクトを利用することになります。これについては次々回以降に解説することにし、次回は分量的な関係で今回説明できなかった、プログラムを用いた予測の自動化・Microsoft Wordとの連携等について解説します。


